Difference between revisions of "Dedekind eta"
From specialfunctionswiki
m (Tom moved page Dedekind eta function to Dedekind eta) |
|||
| Line 7: | Line 7: | ||
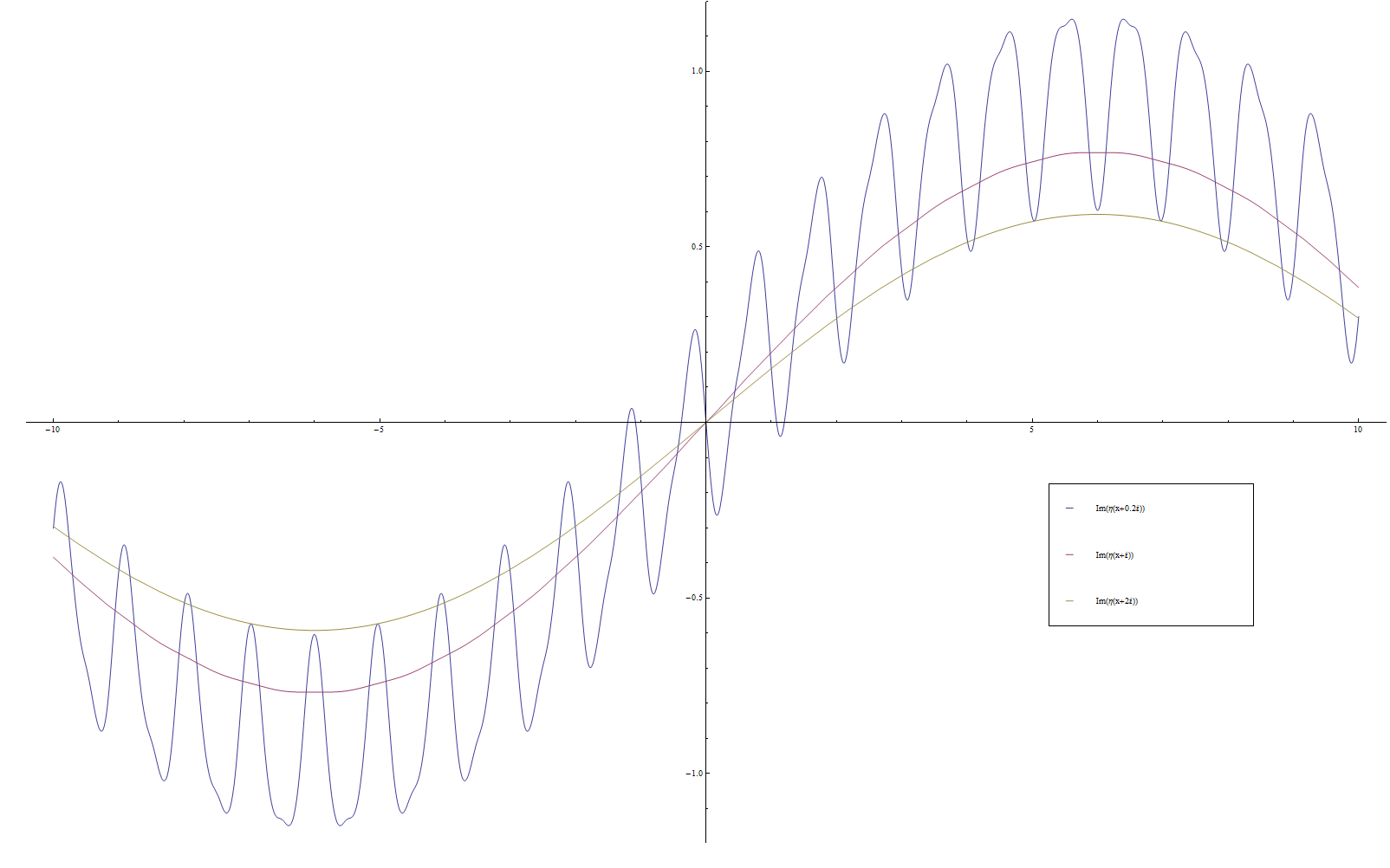
File:DedekindetaIm.png|Imaginary part of $\eta$. | File:DedekindetaIm.png|Imaginary part of $\eta$. | ||
</gallery> | </gallery> | ||
| + | </div> | ||
| + | |||
| + | =Properties= | ||
| + | <div class="toccolours mw-collapsible mw-collapsed"> | ||
| + | <strong>Theorem:</strong> The following formula holds for $\tau$ with $\mathrm{Im} \hspace{2pt} \tau > 0$: | ||
| + | $$\eta \left( -\dfrac{1}{\tau} \right) = (-i\tau)^{\frac{1}{2}}\eta(\tau).$$ | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <strong>Proof:</strong> █ | ||
| + | </div> | ||
</div> | </div> | ||
=References= | =References= | ||
[http://eta.math.georgetown.edu/ A collection of over 6200 identities for the Dedekind Eta Function] | [http://eta.math.georgetown.edu/ A collection of over 6200 identities for the Dedekind Eta Function] | ||
Revision as of 03:55, 7 June 2015
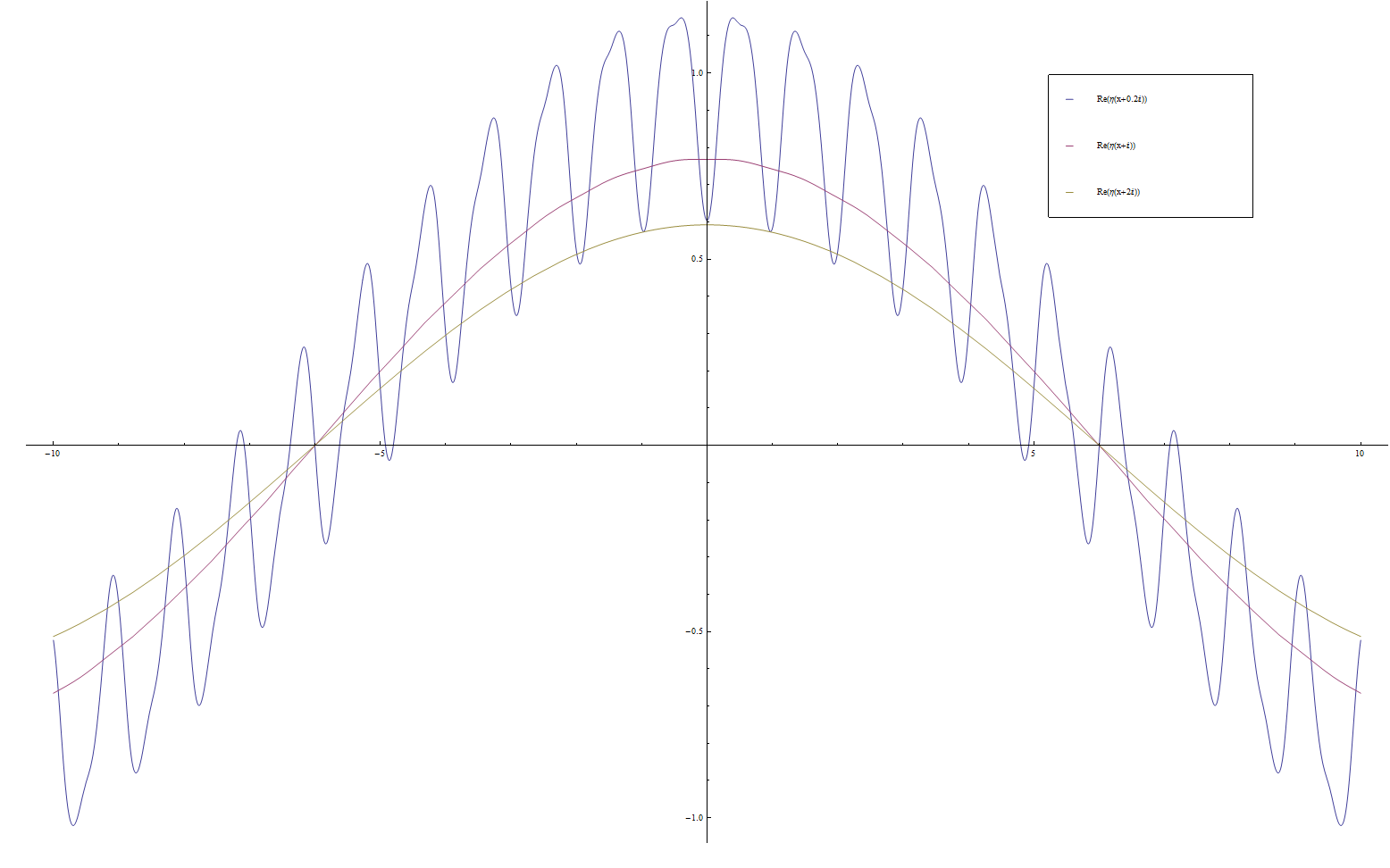
Let $q=e^{2\pi i \tau}$. We define the Dedekind eta function by the formula $$\eta(\tau) = e^{\frac{\pi i \tau}{12}} \displaystyle\prod_{n=1}^{\infty} (1-q^n).$$
Real part of $\eta$.
Imaginary part of $\eta$.
Properties
Theorem: The following formula holds for $\tau$ with $\mathrm{Im} \hspace{2pt} \tau > 0$: $$\eta \left( -\dfrac{1}{\tau} \right) = (-i\tau)^{\frac{1}{2}}\eta(\tau).$$
Proof: █
References
A collection of over 6200 identities for the Dedekind Eta Function
