Difference between revisions of "Modified Bessel K"
From specialfunctionswiki
| Line 2: | Line 2: | ||
$$K_{\nu}(z)=\dfrac{\pi}{2} \dfrac{I_{-\nu}(z)-I_{\nu}(z)}{\sin(\nu \pi)},$$ | $$K_{\nu}(z)=\dfrac{\pi}{2} \dfrac{I_{-\nu}(z)-I_{\nu}(z)}{\sin(\nu \pi)},$$ | ||
where $I_{\nu}$ is the [[Modified Bessel I sub nu|modified Bessel function of the first kind]]. | where $I_{\nu}$ is the [[Modified Bessel I sub nu|modified Bessel function of the first kind]]. | ||
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
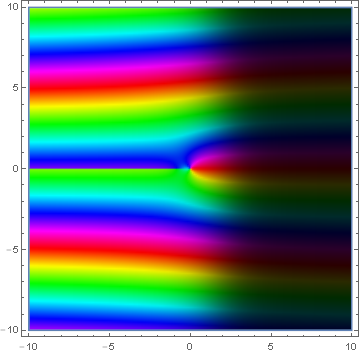
| + | File:Domaincoloringbesselksub1.png|[[Domain coloring]] of $K_1$. | ||
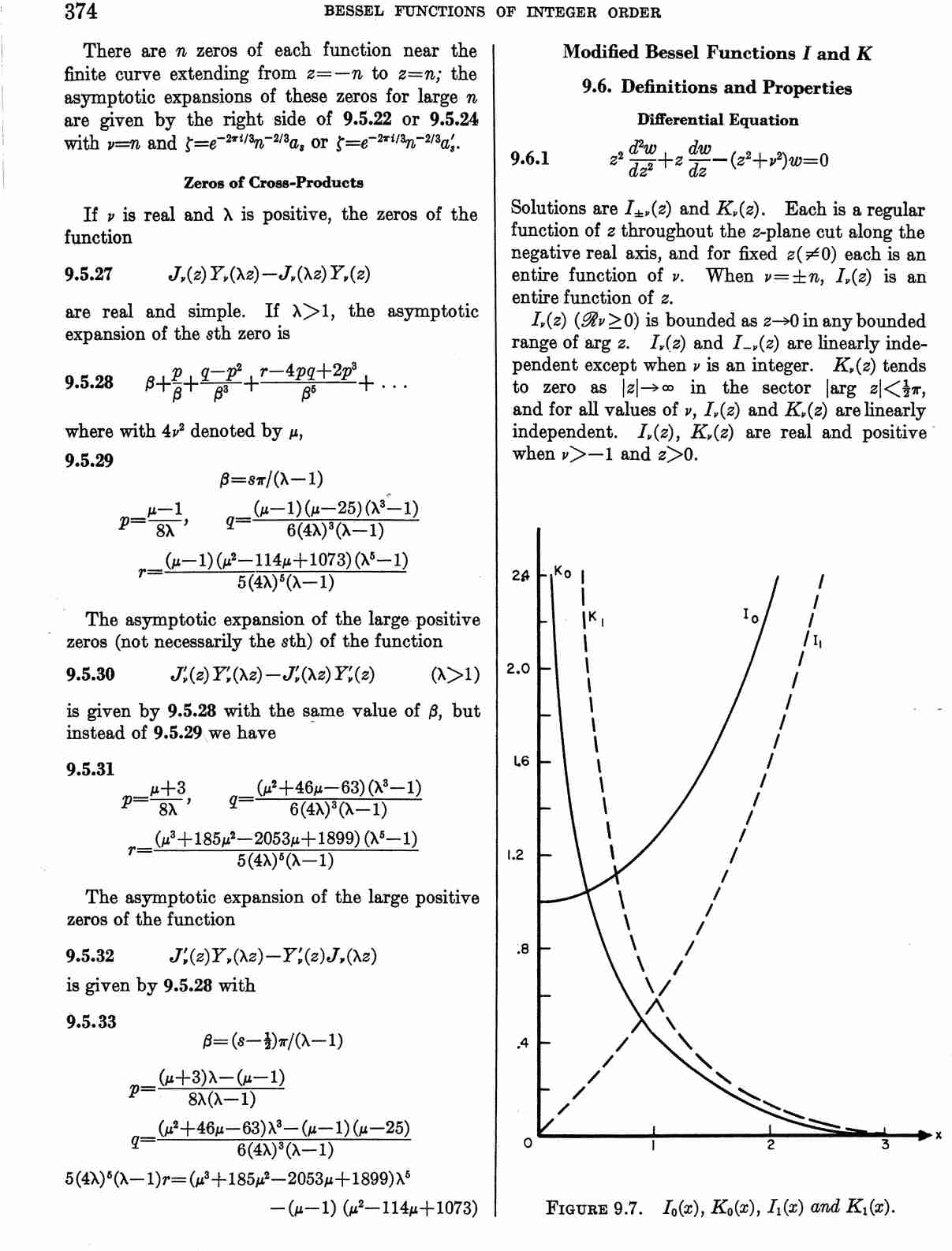
| + | File:Page 374 (Abramowitz&Stegun).jpg|Modified Bessel functions from Abramowitz&Stegun. | ||
| + | </gallery> | ||
| + | </div> | ||
| + | |||
=Properties= | =Properties= | ||
Revision as of 17:50, 25 July 2015
The modified Bessel function of the second kind is defined by $$K_{\nu}(z)=\dfrac{\pi}{2} \dfrac{I_{-\nu}(z)-I_{\nu}(z)}{\sin(\nu \pi)},$$ where $I_{\nu}$ is the modified Bessel function of the first kind.
Domain coloring of $K_1$.
Modified Bessel functions from Abramowitz&Stegun.
.jpg)
Properties
Proposition: The following formula holds: $$K_{\frac{1}{2}}(z)=\sqrt{\dfrac{\pi}{2}}\dfrac{e^{-z}}{\sqrt{z}}; z>0.$$
Proof: █
Theorem
The following formula holds: $$\mathrm{Ai}(z)=\dfrac{1}{\pi} \sqrt{\dfrac{z}{3}} \mathrm{K}_{\frac{1}{3}} \left( \dfrac{2}{3} x^{\frac{3}{2}} \right),$$ where $\mathrm{Ai}$ is the Airy Ai function and $K_{\nu}$ denotes the modified Bessel $K$.
Proof
References
Modified Bessel $K_{\nu}$
