Difference between revisions of "Riemann-Siegel Z"
From specialfunctionswiki
(Created page with "The Riemann-Siegel $Z$ function is defined by $$Z(t)=e^{i\theta(t)}\zeta \left( \dfrac{1}{2}+it \right),$$ where $\theta$ denotes the Riemann-Siegel theta function and $\z...") |
|||
| Line 2: | Line 2: | ||
$$Z(t)=e^{i\theta(t)}\zeta \left( \dfrac{1}{2}+it \right),$$ | $$Z(t)=e^{i\theta(t)}\zeta \left( \dfrac{1}{2}+it \right),$$ | ||
where $\theta$ denotes the [[Riemann-Siegel theta function]] and $\zeta$ denotes the [[Riemann zeta function]]. | where $\theta$ denotes the [[Riemann-Siegel theta function]] and $\zeta$ denotes the [[Riemann zeta function]]. | ||
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
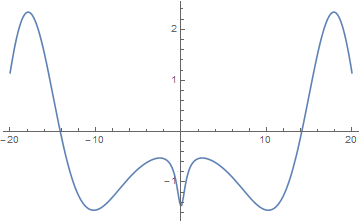
| + | File:Plot riemann siegel z.png|Graph of $Z(t)$ on $[-20,20]$. | ||
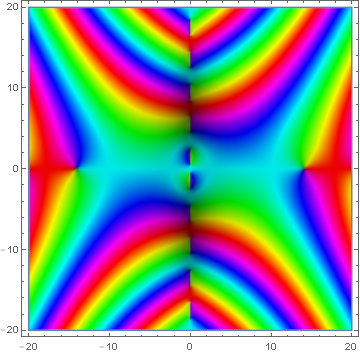
| + | File:Domain coloring riemann siegel z.png|[[Domain coloring]] of [[analytic continuation]] of $Z(t)$. | ||
| + | </gallery> | ||
| + | </div> | ||
Revision as of 19:19, 25 July 2015
The Riemann-Siegel $Z$ function is defined by $$Z(t)=e^{i\theta(t)}\zeta \left( \dfrac{1}{2}+it \right),$$ where $\theta$ denotes the Riemann-Siegel theta function and $\zeta$ denotes the Riemann zeta function.
Domain coloring of analytic continuation of $Z(t)$.