Difference between revisions of "Takagi function"
From specialfunctionswiki
| Line 1: | Line 1: | ||
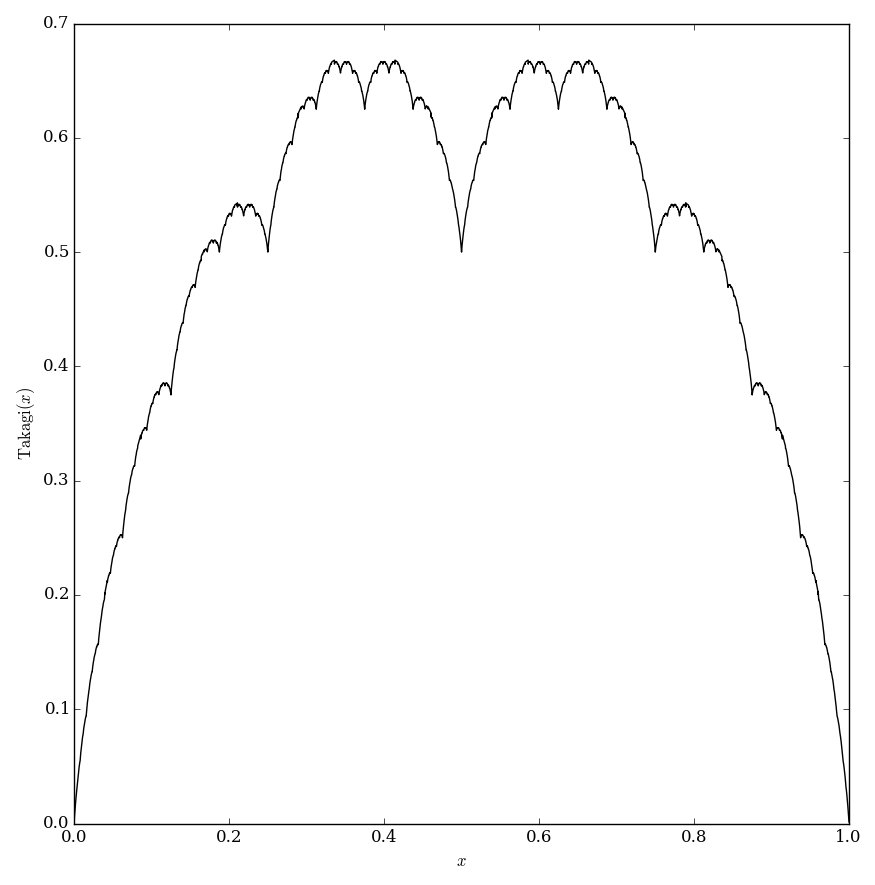
| − | + | The Takagi function (also called the blancmange function) is defined by | |
| − | $$\mathrm{takagi}(x)=\displaystyle\sum_{k=0}^{\infty} \dfrac{ | + | $$\mathrm{takagi}(x)=\displaystyle\sum_{k=0}^{\infty} \dfrac{\mathrm{dist}_{\mathbb{Z}}(2^n x)}{2^n}.$$ |
| − | |||
<div align="center"> | <div align="center"> | ||
<gallery> | <gallery> | ||
Revision as of 03:13, 6 July 2016
The Takagi function (also called the blancmange function) is defined by $$\mathrm{takagi}(x)=\displaystyle\sum_{k=0}^{\infty} \dfrac{\mathrm{dist}_{\mathbb{Z}}(2^n x)}{2^n}.$$
Properties
Theorem: The Takagi function is continuous on $\mathbb{R}$.
Proof: █
Theorem: The Takagi function is nowhere differentiable on $\mathbb{R}$.
Proof: █