Difference between revisions of "Takagi function"
From specialfunctionswiki
| Line 8: | Line 8: | ||
=Properties= | =Properties= | ||
| − | + | [[Takagi function is continuous]]<br /> | |
| − | + | [[Takagi function is nowhere differentiable]]<br /> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
=See Also= | =See Also= | ||
Revision as of 03:14, 6 July 2016
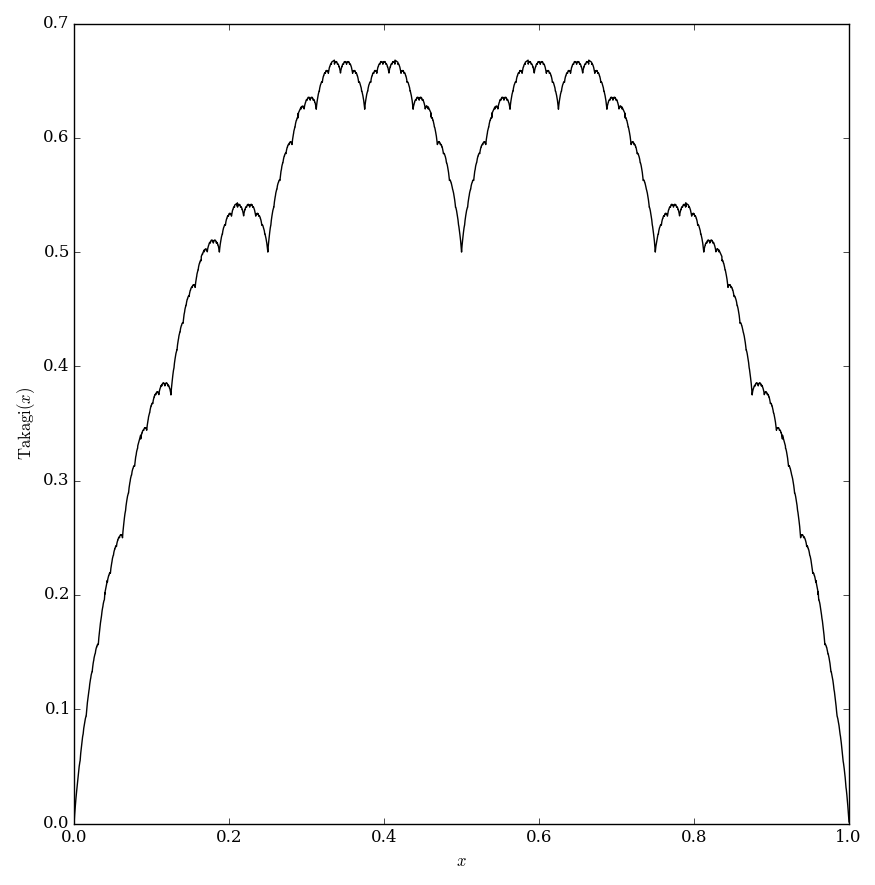
The Takagi function (also called the blancmange function) is defined by $$\mathrm{takagi}(x)=\displaystyle\sum_{k=0}^{\infty} \dfrac{\mathrm{dist}_{\mathbb{Z}}(2^n x)}{2^n}.$$
Graph of $\mathrm{takagi}$ on $[0,1]$.
Properties
Takagi function is continuous
Takagi function is nowhere differentiable
