Difference between revisions of "Van der Waerden function"

From specialfunctionswiki
Jump to: navigation, search
Line 1: Line 1:
−
Define $s(x)=\inf_{n \in \mathbb{Z}} |x-n|$ (i.e. the distance from $x$ to the set of integers $\mathbb{Z}$). The van der Waerden function is defined by the formula
+
The van der Waerden function $V \colon \mathbb{R} \rightarrow \mathbb{R}$ is defined by the formula
−
$$V(x)=\displaystyle\sum_{k=0}^{\infty} \dfrac{s \left(10^k x \right)}{10^k}.$$
+
$$V(x)=\displaystyle\sum_{k=0}^{\infty} \dfrac{\mathrm{dist}_{\mathbb{Z}} \left(10^k x \right)}{10^k},$$
−
Note: to calculate $s(x)$ you may use $s(x)=\min \left(2^n x - \lfloor 2^n x \rfloor, \lceil 2^n x \rceil - x \right)$, where $\lfloor \cdot \rfloor$ denotes the [[floor]] function and $\lceil \cdot \rceil$ denotes the [[ceiling]] function.
+
where $\mathrm{dist}_{\mathbb{Z}}$ denotes the [[distance to integers]] function.
−
 
 
  
  

Revision as of 03:19, 6 July 2016

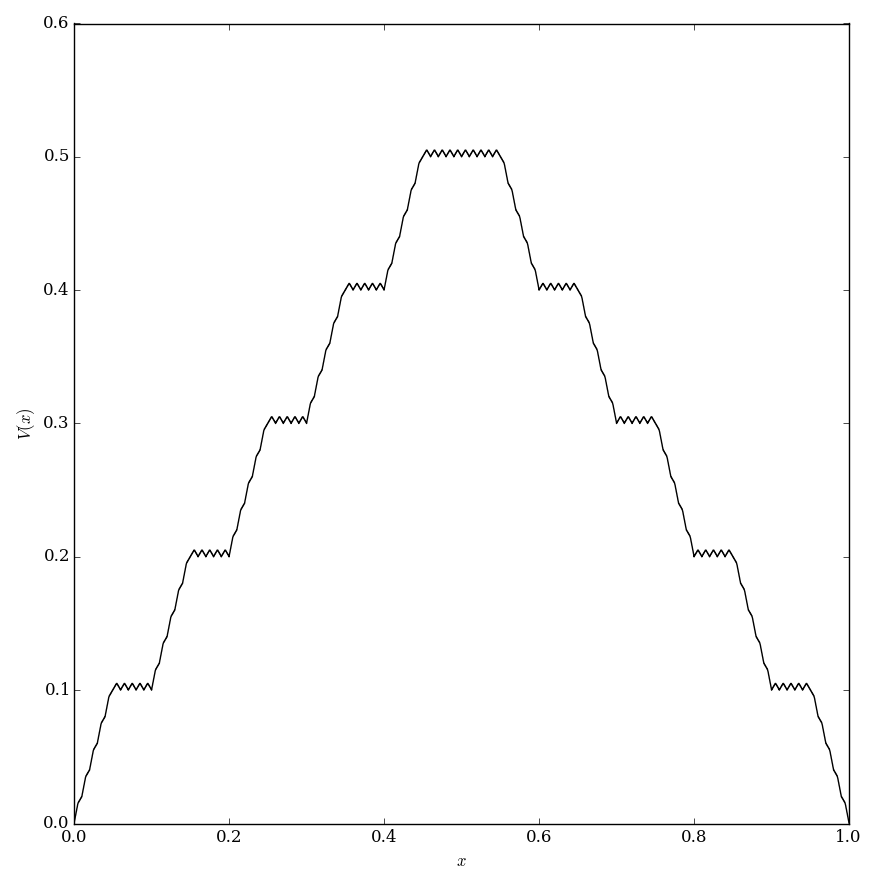
The van der Waerden function $V \colon \mathbb{R} \rightarrow \mathbb{R}$ is defined by the formula $$V(x)=\displaystyle\sum_{k=0}^{\infty} \dfrac{\mathrm{dist}_{\mathbb{Z}} \left(10^k x \right)}{10^k},$$ where $\mathrm{dist}_{\mathbb{Z}}$ denotes the distance to integers function.


  • Plot of the van der Waerden function.

Properties

van der Waerden function is continuous
van der Waerden function is nowhere differentiable

See Also

Takagi function

References

[1]

Retrieved from "http://specialfunctionswiki.org/index.php?title=Van_der_Waerden_function&oldid=7140"