Difference between revisions of "Chebyshev theta function"
From specialfunctionswiki
| Line 7: | Line 7: | ||
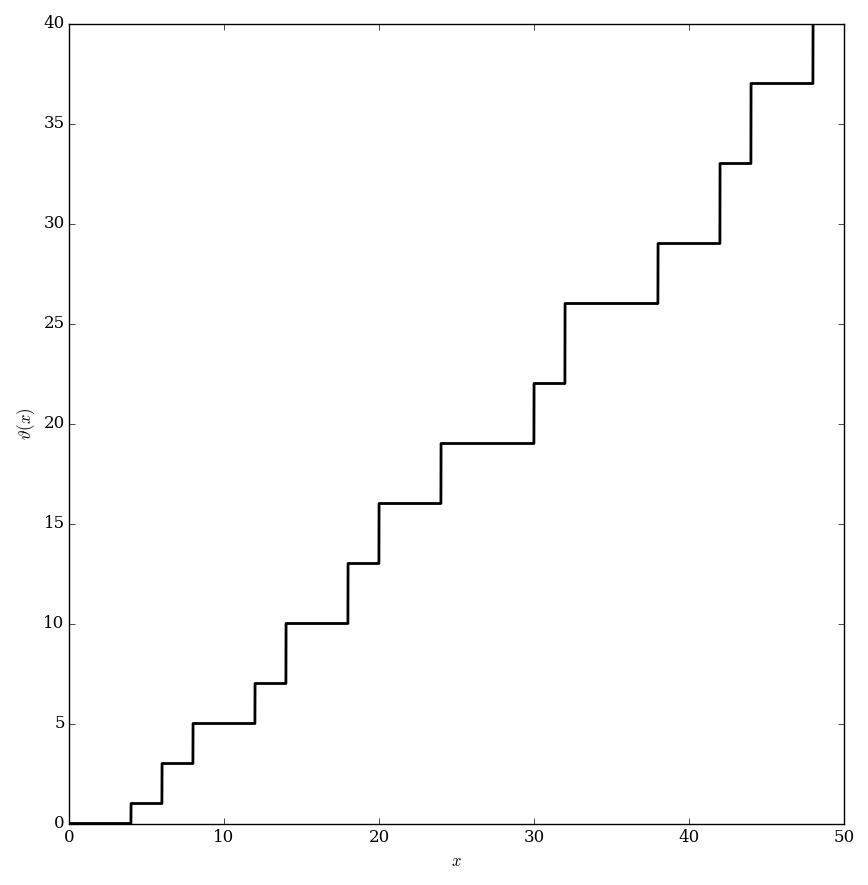
File:Chebyshevplotfrom0to50.png|Plot of $\vartheta$ on $[0,50]$. | File:Chebyshevplotfrom0to50.png|Plot of $\vartheta$ on $[0,50]$. | ||
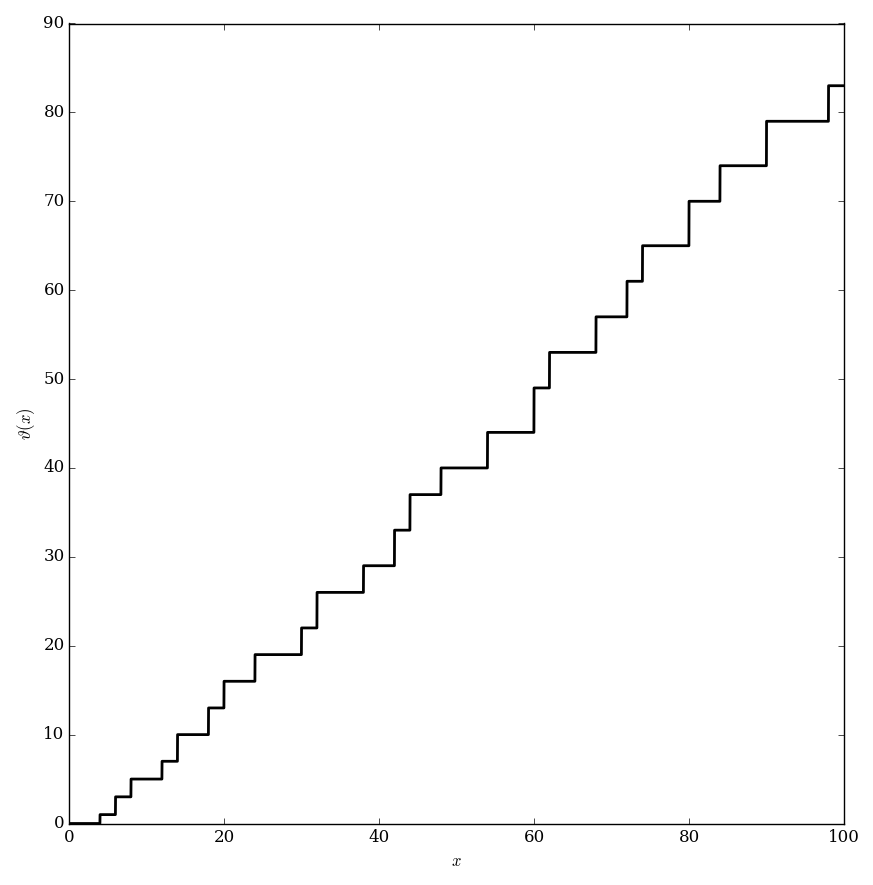
File:Chebyshevplotfrom0to100.png|Plot of $\vartheta$ on $[0,100]$. | File:Chebyshevplotfrom0to100.png|Plot of $\vartheta$ on $[0,100]$. | ||
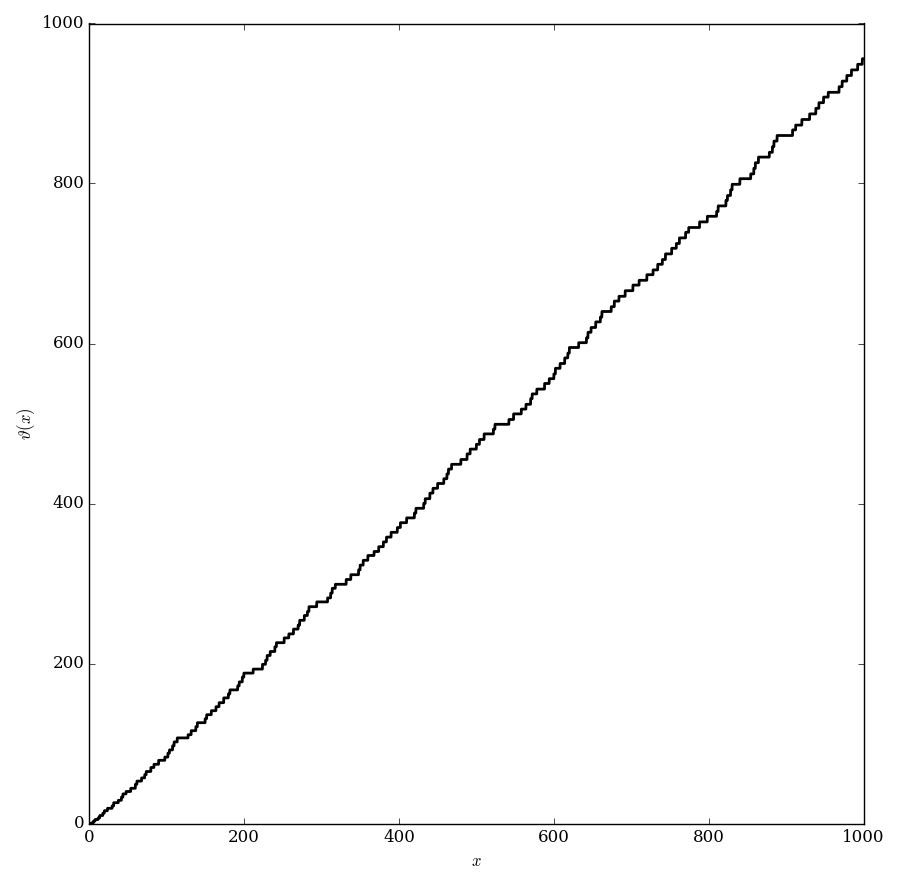
| − | File: | + | File:Chebyshevplotfrom0to1000.png|Plot of $\vartheta$ on $[0,1000]$. |
</gallery> | </gallery> | ||
</div> | </div> | ||
Revision as of 02:13, 28 November 2016
The Chebyshev $\vartheta$ function is $$\vartheta(x) = \displaystyle\sum_{p \leq x} \log p,$$ where $p \leq x$ denotes that $p$ is a prime number less than the real number $x$.