Difference between revisions of "Arccosh"
From specialfunctionswiki
(→Properties) |
|||
| Line 12: | Line 12: | ||
=Properties= | =Properties= | ||
[[Derivative of arccosh]] <br /> | [[Derivative of arccosh]] <br /> | ||
| + | [[Antiderivative of arccosh]]<br /> | ||
=See Also= | =See Also= | ||
Latest revision as of 23:42, 11 December 2016
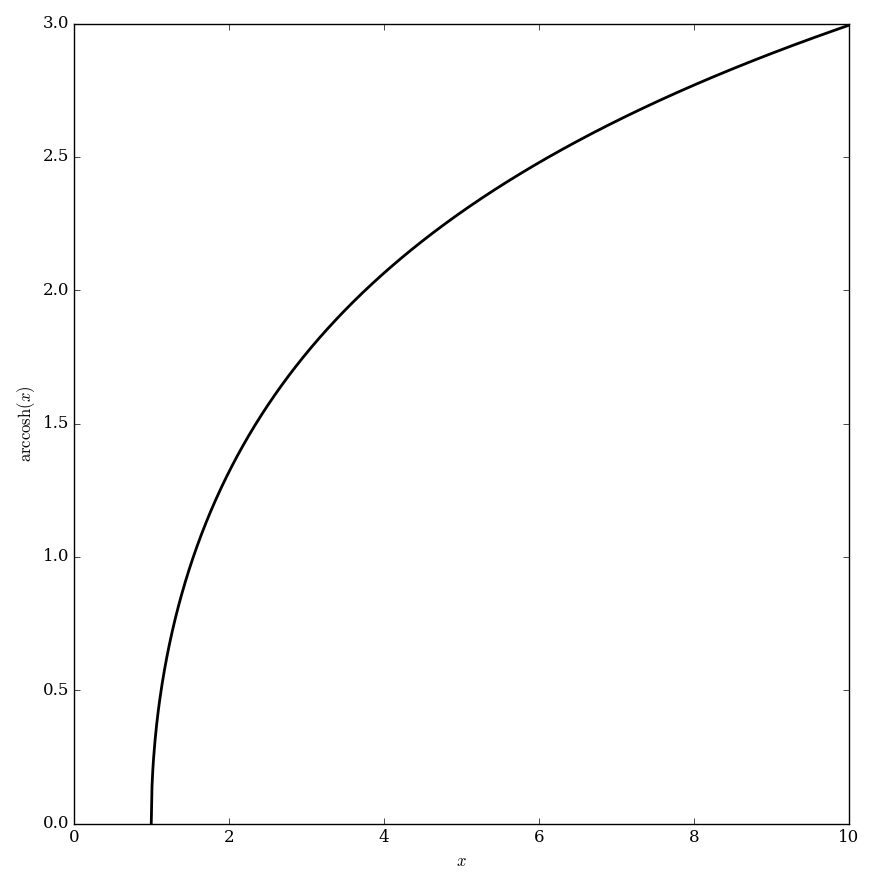
The inverse hyperbolic cosine function $\mathrm{arccosh}$ is the inverse function of the hyperbolic cosine function. It may be defined by $$\mathrm{arccosh}(z)=\log \left(z + \sqrt{1+z^2} \right),$$ where $\log$ denotes the logarithm.
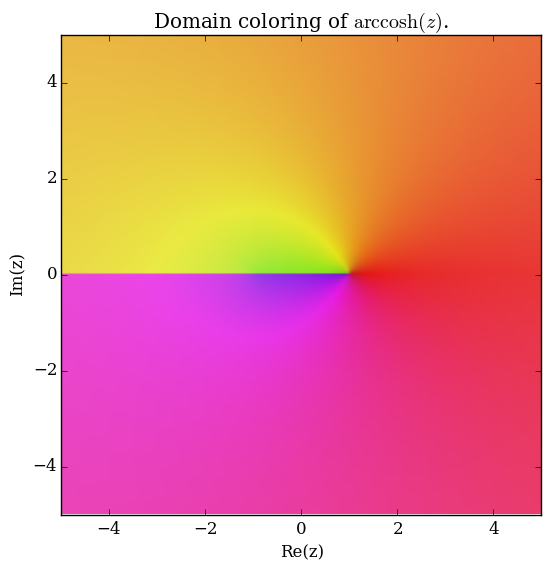
Domain coloring of $\mathrm{arccosh}$.
Properties
Derivative of arccosh
Antiderivative of arccosh