Difference between revisions of "Dilogarithm"
From specialfunctionswiki
(→Properties) |
|||
| Line 21: | Line 21: | ||
* {{BookReference|Higher Transcendental Functions Volume I|1953|Harry Bateman|prev=findme|next=Relationship between dilogarithm and log(1-z)/z}}: $\S 1.11.1 (22)$ | * {{BookReference|Higher Transcendental Functions Volume I|1953|Harry Bateman|prev=findme|next=Relationship between dilogarithm and log(1-z)/z}}: $\S 1.11.1 (22)$ | ||
* {{BookReference|Dilogarithms and Associated Functions|1958|Leonard Lewin|next=Taylor series of log(1-z)}}: $(1.1)$ | * {{BookReference|Dilogarithms and Associated Functions|1958|Leonard Lewin|next=Taylor series of log(1-z)}}: $(1.1)$ | ||
| + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=findme|next=findme}}: $27.7.2$ (<i>note: writes $\mathrm{Li}_2$ as $\sum_{k=1}^{\infty} \frac{(-1)^k(x-1)^k}{k^2}$ for $0 \leq x \leq 2$, equivalent to our definition on $\mathbb{R}$</i>) | ||
* {{BookReference|Polylogarithms and Associated Functions|1981|ed=2nd|edpage=Second Edition|Leonard Lewin|next=Taylor series of log(1-z)}}: $(1.1)$ | * {{BookReference|Polylogarithms and Associated Functions|1981|ed=2nd|edpage=Second Edition|Leonard Lewin|next=Taylor series of log(1-z)}}: $(1.1)$ | ||
* {{BookReference|Structural Properties of Polylogarithms|1991|Leonard Lewin|next=Relationship between dilogarithm and log(1-z)/z}}: $(1.1)$ | * {{BookReference|Structural Properties of Polylogarithms|1991|Leonard Lewin|next=Relationship between dilogarithm and log(1-z)/z}}: $(1.1)$ | ||
Revision as of 02:26, 21 December 2017
The dilogarithm function $\mathrm{Li}_2$ is defined for $|z| \leq 1$ by $$\mathrm{Li}_2(z)=\displaystyle\sum_{k=1}^{\infty} \dfrac{z^k}{k^2},$$ which is a special case of the polylogarithm.
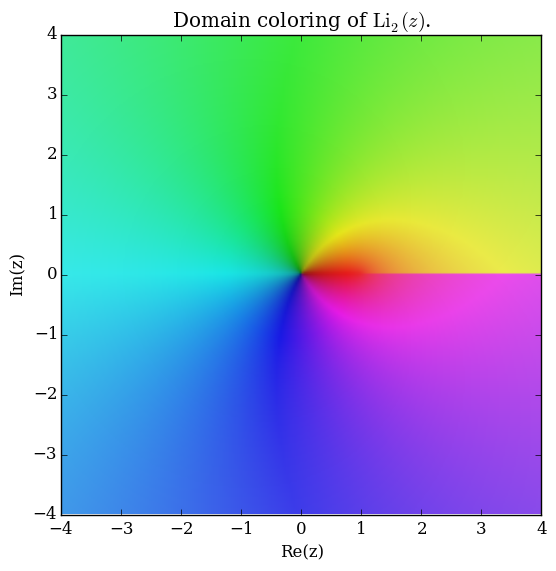
Domain coloring of $\mathrm{Li}_2$.
Properties
Relationship between dilogarithm and log(1-z)/z
Relationship between Li 2(1),Li 2(-1), and pi
Li 2(1)=pi^2/6
Relationship between Li 2(-1/x),Li 2(-x),Li 2(-1), and log^2(x)
Derivative of Li 2(-1/x)
Li2(z)=zPhi(z,2,1)
Li 2(z)=-Li 2(1/z)-(1/2)(log z)^2 + i pi log(z) + pi^2/3
References
- 1953: Harry Bateman: Higher Transcendental Functions Volume I ... (previous) ... (next): $\S 1.11.1 (22)$
- 1958: Leonard Lewin: Dilogarithms and Associated Functions ... (next): $(1.1)$
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $27.7.2$ (note: writes $\mathrm{Li}_2$ as $\sum_{k=1}^{\infty} \frac{(-1)^k(x-1)^k}{k^2}$ for $0 \leq x \leq 2$, equivalent to our definition on $\mathbb{R}$)
- 1981: Leonard Lewin: Polylogarithms and Associated Functions (2nd ed.) ... (next): $(1.1)$
- 1991: Leonard Lewin: Structural Properties of Polylogarithms ... (next): $(1.1)$
(page 31)
The Dilogarithm function
[1]