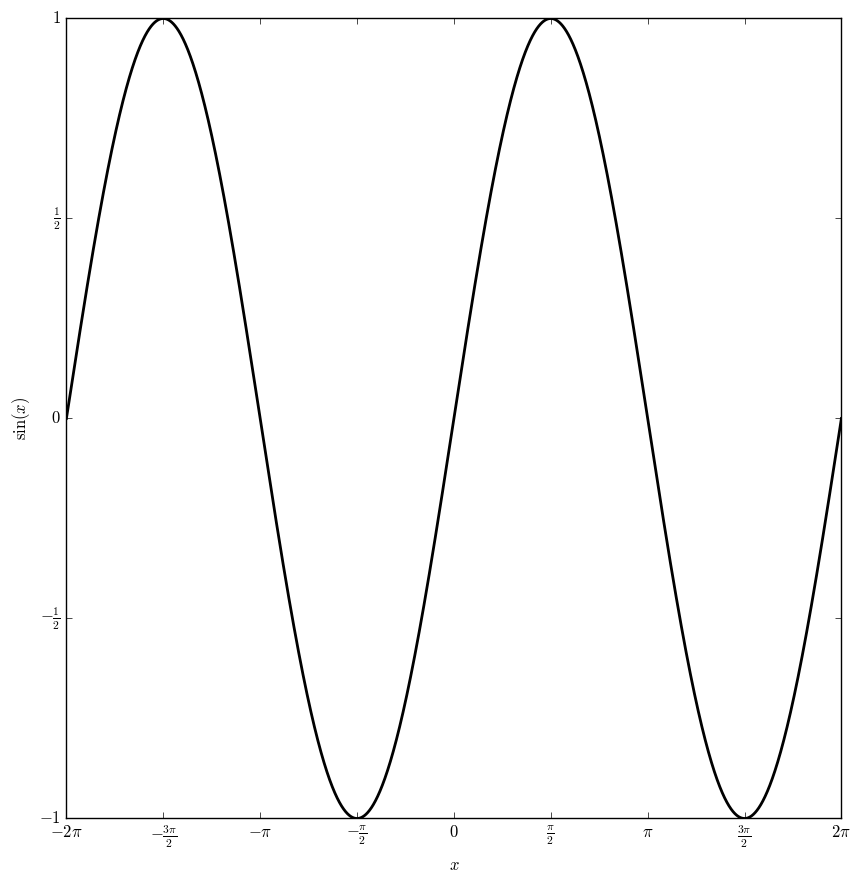
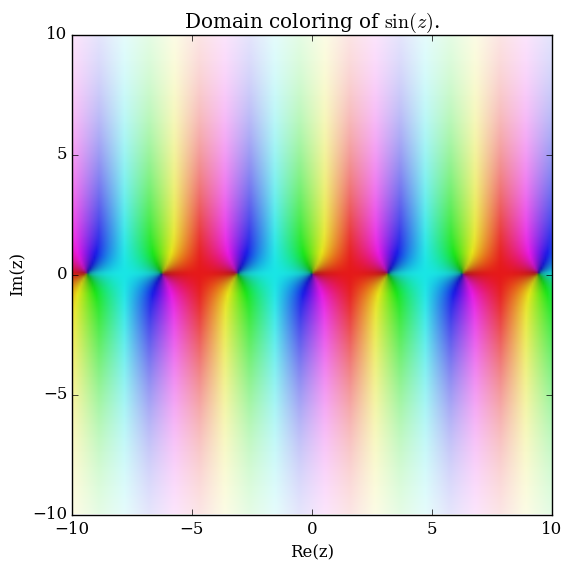
Sine
From specialfunctionswiki
The sine function $\sin \colon \mathbb{C} \rightarrow \mathbb{C}$ is defined by $$\sin(z)=\dfrac{e^{iz}-e^{-iz}}{2i},$$ where $e^z$ is the exponential function.
Graph of $\sin$ on $[-2\pi,2\pi]$.
Domain coloring of $\sin$.
Contents
Properties
Derivative of sine Pythagorean identity for sin and cos Taylor series of sine Weierstrass factorization of sine Gamma-Sine_Relation Beta in terms of sine and cosine Relationship between sine and hypergeometric 0F1 Relationship between spherical Bessel j sub nu and sine Relationship between sin and sinh Relationship between sinh and sin Relationship between sine, Gudermannian, and tanh Relationship between tanh, inverse Gudermannian, and sin
See Also
Videos
References
The sine product formula and the gamma function
