Polygamma

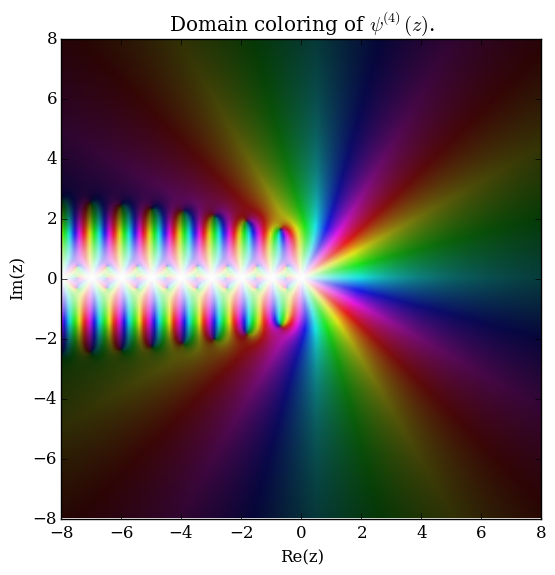
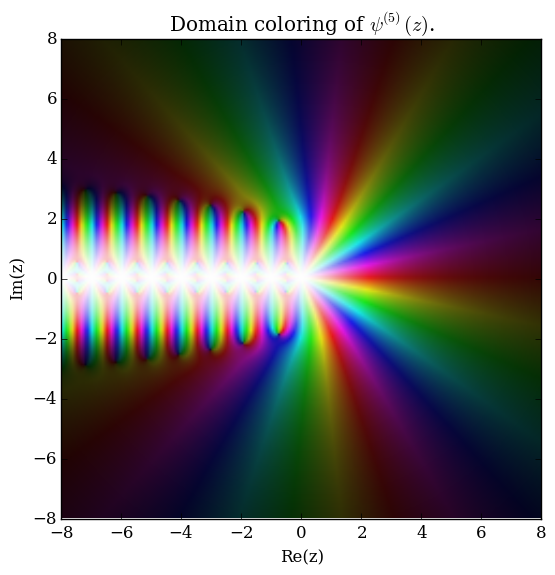
The polygamma function of order $m$, $\psi^{(m)}(z) \colon \mathbb{C} \setminus \{0,-1,-2,\ldots\} \rightarrow \mathbb{C}$, is defined by the formula $$\psi^{(m)}(z) = \dfrac{\mathrm{d}^{m+1}}{\mathrm{d}z^{m+1}} \log \Gamma(z),$$ where $\log \Gamma$ denotes the loggamma function. The digamma function $\psi$ is the function $\psi^{(0)}(z)$ and the trigamma function is $\psi^{(1)}(z)$.

• 

  Domain coloring of $\psi^{(0)}(z)$.

• 

  Domain coloring of $\psi^{(1)}(z)$.

• 

  Domain coloring of $\psi^{(2)}(z)$.

• 

  Domain coloring of $\psi^{(3)}(z)$.

• 

  Domain coloring of $\psi^{(4)}(z)$.

• 

  Domain coloring of $\psi^{(5)}(z)$.

Properties

Integral representation of polygamma
Integral representation of polygamma 2
Polygamma recurrence relation
Polygamma reflection relation
Polygamma series representation
Relation between polygamma and Hurwitz zeta

See Also

Digamma
Trigamma

References

• 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 6.4.1