Dedekind eta
From specialfunctionswiki
Revision as of 07:08, 19 January 2015 by Tom (talk | contribs) (Tom moved page Dedekind eta function to Dedekind eta)
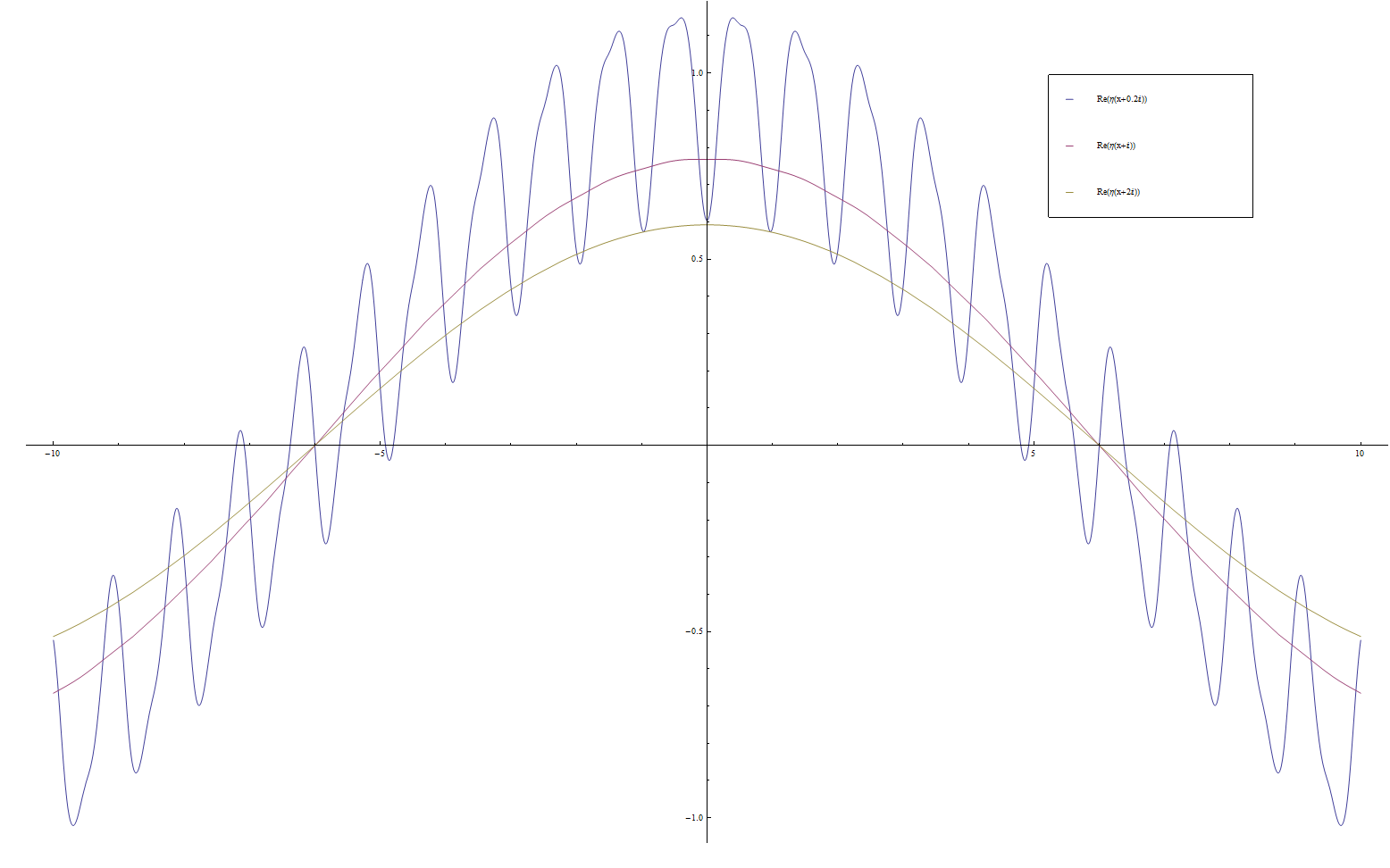
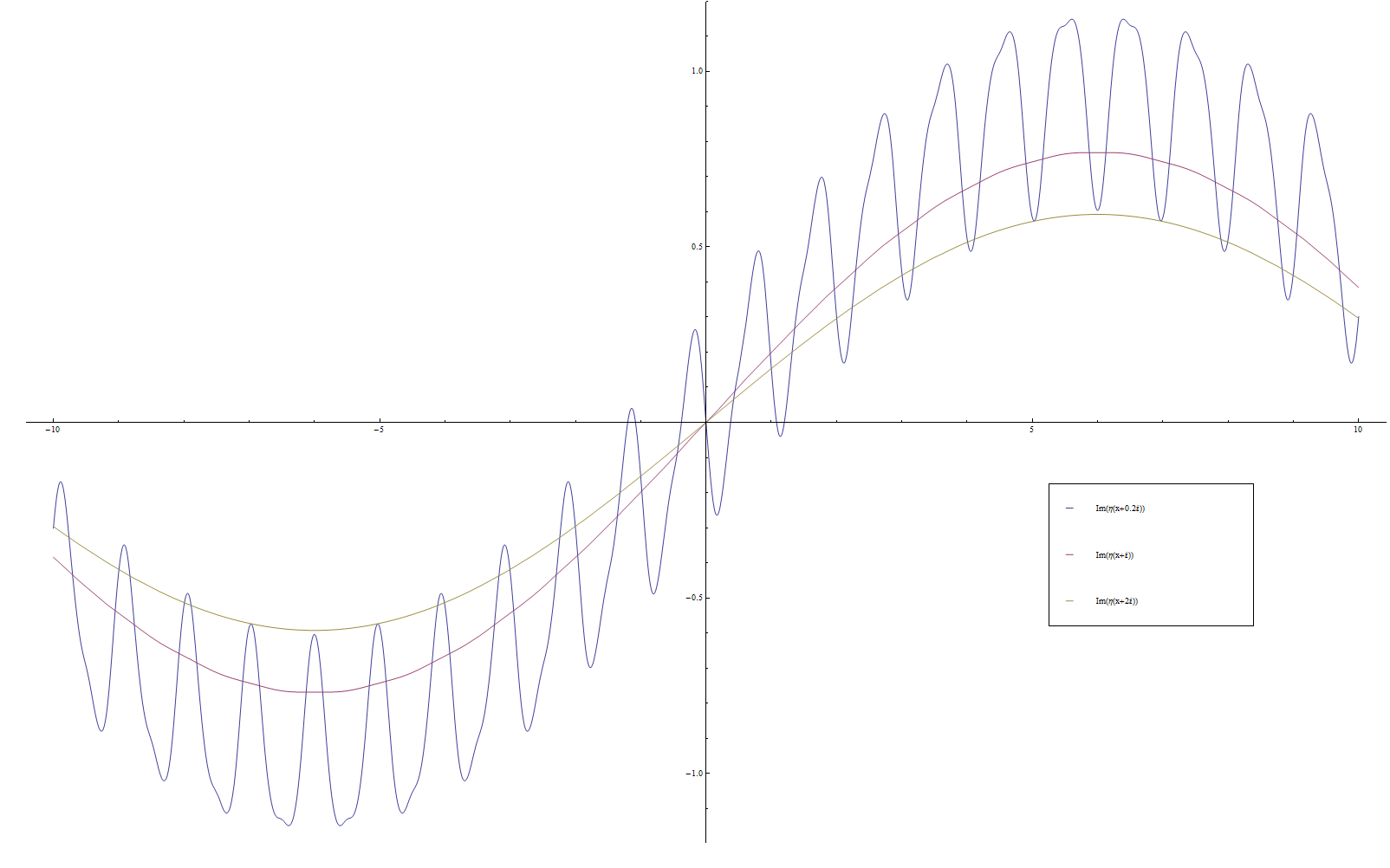
Let $q=e^{2\pi i \tau}$. We define the Dedekind eta function by the formula $$\eta(\tau) = e^{\frac{\pi i \tau}{12}} \displaystyle\prod_{n=1}^{\infty} (1-q^n).$$
References
A collection of over 6200 identities for the Dedekind Eta Function