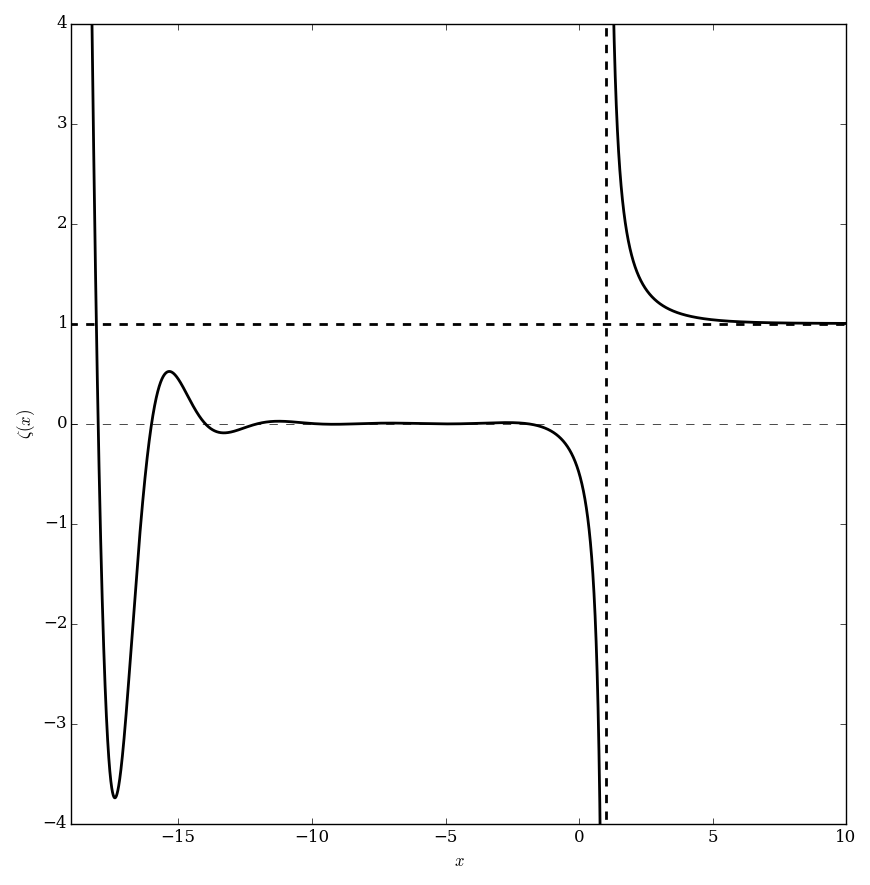
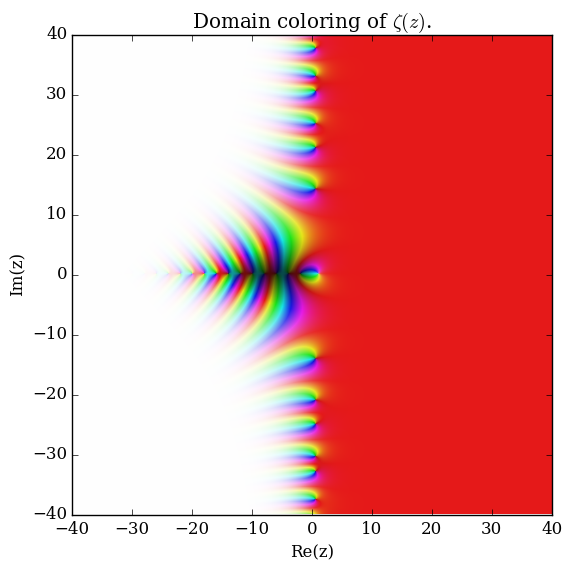
Riemann zeta
The Riemann zeta function $\zeta$ is defined for $\mathrm{Re}(z)>1$ by $$\zeta(z) = \displaystyle\sum_{n=1}^{\infty} \dfrac{1}{n^z}.$$
Graph of $\zeta$ on $[-21,10] \setminus \{1\}$.
Domain coloring of $\zeta$.
Properties
Derivative of Riemann zeta
Euler product for Riemann zeta
Laurent series of the Riemann zeta function
Relationship between prime zeta, Möbius function, logarithm, and Riemann zeta
Series for log(riemann zeta) over primes
Series for log(Riemann zeta) in terms of Mangoldt function
Logarithmic derivative of Riemann zeta in terms of series over primes
Logarithmic derivative of Riemann zeta in terms of Mangoldt function
Reciprocal Riemann zeta in terms of Mobius
Riemann zeta as integral of monomial divided by an exponential
Videos
Riemann Zeta function playlist (8 March 2012)
Möbius Inversion of $\zeta(s)$ (3 July 2016)
Zeta Integral (5 July 2016)
External links
- 15 Videos about the Riemann $\zeta$ function
- English translation of Riemann's paper "On the number of prime numbers less than a given quantity"
- Evaluating $\zeta(2)$
- The Riemann Hypothesis: FAQ and resources
- How Euler discovered the zeta function
- Andrew Odlyzko: Tables of zeros of the Riemann zeta function
See also
References
- 1930: Edward Charles Titchmarsh: The Zeta-Function of Riemann ... (next): § Introduction $(1)$
- 1953: Harry Bateman: Higher Transcendental Functions Volume III ... (previous) ... (next): pg. $170$
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $23.2.1$
