Struve function
From specialfunctionswiki
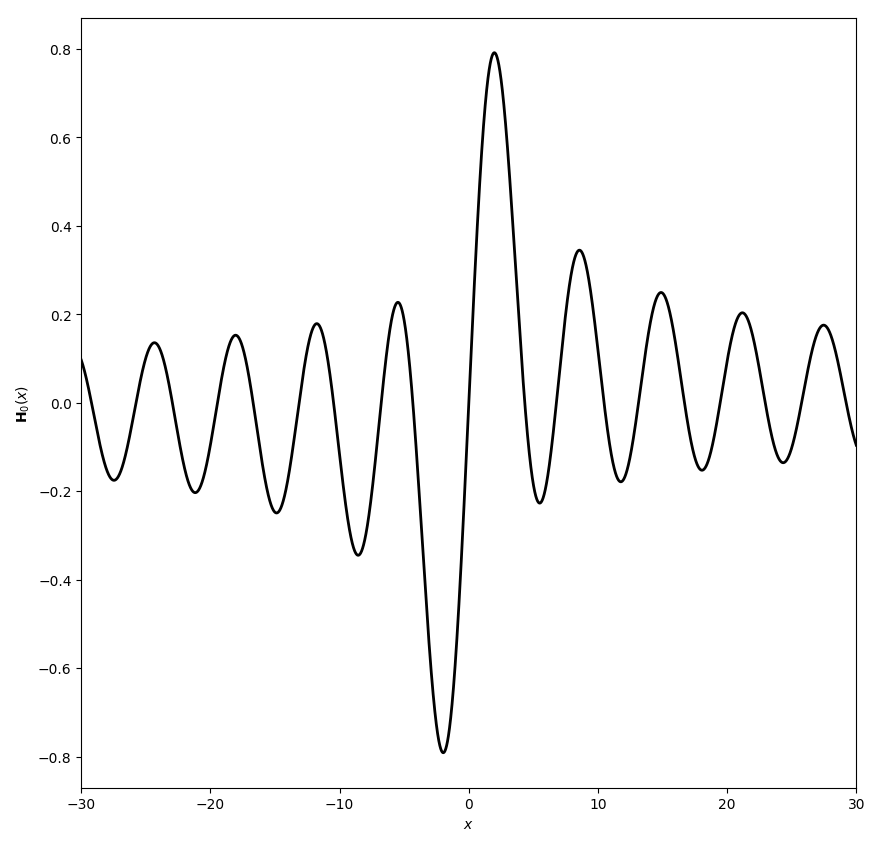
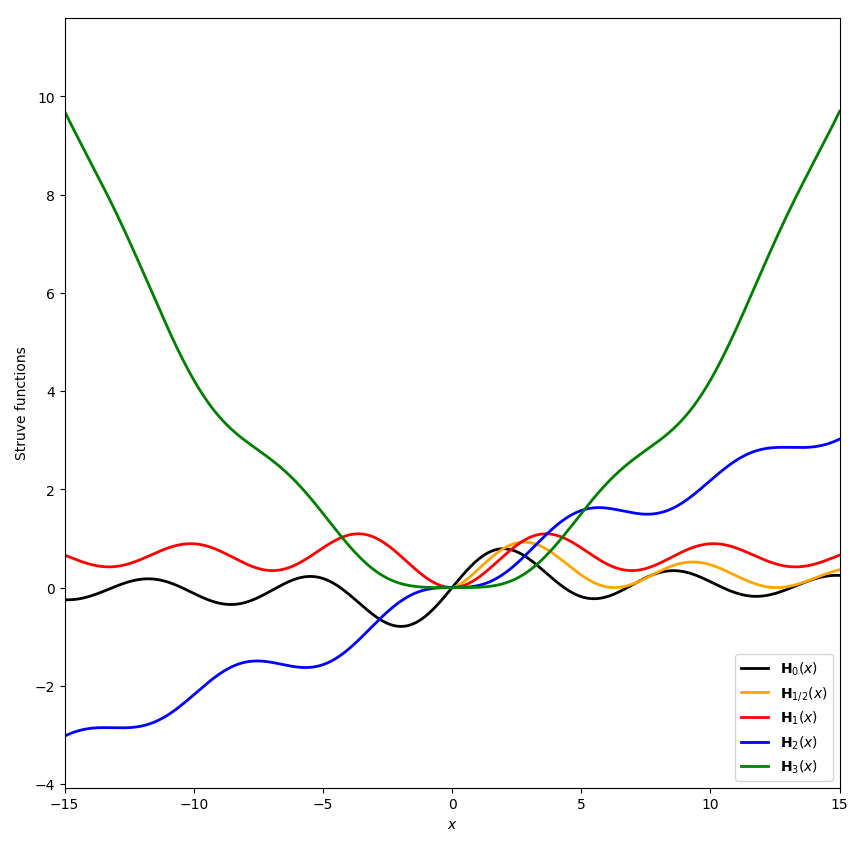
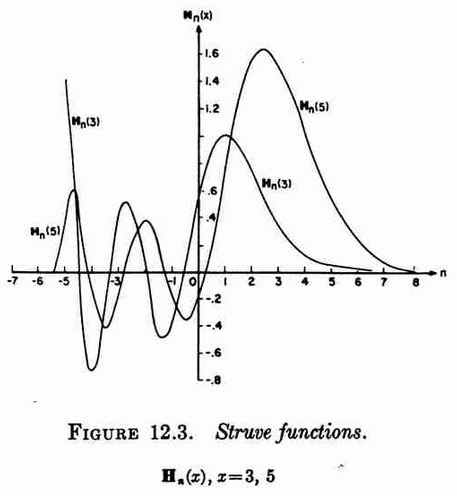
The Struve functions are defined by $$\mathbf{H}_{\nu}(z)=\left(\dfrac{z}{2}\right)^{\nu+1} \displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k\left(\frac{z}{2}\right)^{2k}}{\Gamma(k+\frac{3}{2})\Gamma \left(k+\nu+\frac{3}{2} \right)}.$$
Properties
Relationship between Struve function and hypergeometric pFq
Relationship between Weber function 0 and Struve function 0
Relationship between Weber function 1 and Struve function 1
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $12.1.3$