Arctan
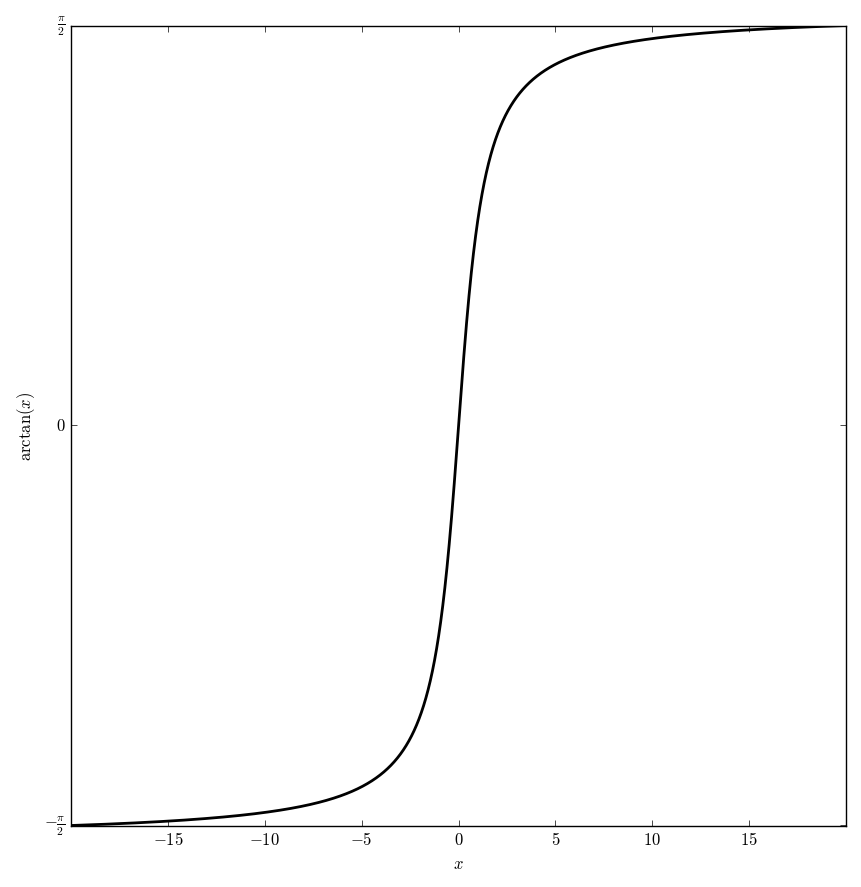
The $\mathrm{arctan}$ function is the inverse function of the tangent function.
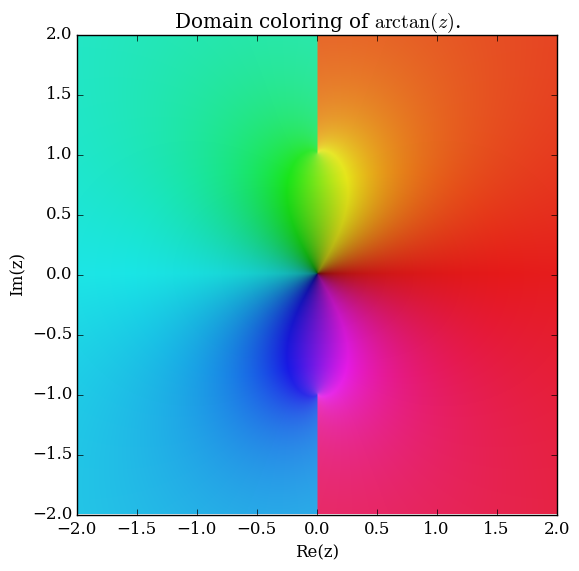
Domain coloring of $\mathrm{arctan}$.
Contents
Properties
Theorem
The following formula holds: $$\dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{arctan}(z) = \dfrac{1}{z^2+1},$$ where $\mathrm{arctan}$ denotes the inverse tangent function.
Proof
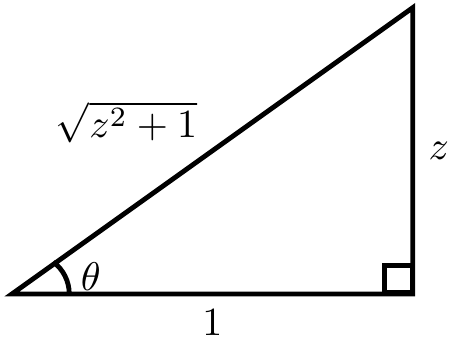
If $\theta=\mathrm{arctan}(z)$ then $\tan \theta = z$. Now implicit differentiation with respect to $z$ yields $$\sec^2(\theta)\theta'=1.$$ The following triangle shows that $\sec^2(\mathrm{arctan}(z))=z^2+1$:
Substituting back in $\theta=\mathrm{arccos(z)}$ yields the formula $$\dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{arccos(z)} = \dfrac{1}{\sec^2(\mathrm{arctan(z)})} = \dfrac{1}{z^2+1},$$ as was to be shown. █
References
Theorem
The following formula holds: $$\displaystyle\int \mathrm{arctan}(z) \mathrm{d}z = z\mathrm{arctan}(z) - \dfrac{1}{2}\log \left(z^2+1 \right)+C,$$ where $\mathrm{arctan}$ denotes the inverse tangent and $\log$ denotes the logarithm.
Proof
Let $u=\mathrm{arctan}(z)$ and $\mathrm{d}v=1$. Then $v=z$ and because of the derivative of arctan, $\mathrm{d}u=\dfrac{1}{z^2+1} \mathrm{d}z$. Therefore using integration by parts, $$\displaystyle\int \mathrm{arctan}(z) \mathrm{d}z = z \mathrm{arctan}(z) - \displaystyle\int \dfrac{z}{z^2+1} \mathrm{d}z.$$ To evaluate the remaining integral, let $w=z^2+1$ so that $\mathrm{d}w=2z \mathrm{d}z$, i.e. $\dfrac{1}{2} \mathrm{d} w = z \mathrm{d}z$ and we see using the derivative of the logarithm, $$\displaystyle\int \mathrm{arctan}(z) \mathrm{d}z = z \mathrm{arctan}(z) - \dfrac{1}{2}\displaystyle\int \dfrac{1}{w} \mathrm{d}w = z \mathrm{arctan}(z) - \dfrac{1}{2} \log(z^2+1) + C,$$ as was to be shown.
References
Theorem
The following formula holds: $$\mathrm{arctan}(z) = \mathrm{arccot}\left( \dfrac{1}{z} \right),$$ where $\mathrm{arctan}$ denotes the inverse tangent and $\mathrm{arccot}$ denotes the inverse cotangent.
Proof
Let $y = \arctan \left( \dfrac{1}{z} \right)$. Then since arctan is the inverse function of tangent, $$\tan(y)=\dfrac{1}{z}.$$ By the definition of cotangent, we get $$\cot(y)=z.$$ Since $\mathrm{arccot}$ is the inverse function of $\cot$, take the $\mathrm{arccot}$ of each side to get $$y = \mathrm{arccot}(z).$$ Therefore we have shown $$\arctan \left( \dfrac{1}{z} \right) = \mathrm{arccot}(z),$$ as was to be shown.