Difference between revisions of "Polygamma"
(→Properties) |
|||
| (14 intermediate revisions by the same user not shown) | |||
| Line 13: | Line 13: | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
| + | |||
| + | =Properties= | ||
| + | [[Integral representation of polygamma for Re(z) greater than 0]]<br /> | ||
| + | [[Integral representation of polygamma 2]]<br /> | ||
| + | [[Polygamma recurrence relation]]<br /> | ||
| + | [[Polygamma reflection formula]]<br /> | ||
| + | [[Polygamma multiplication formula]]<br /> | ||
| + | [[Polygamma series representation]]<br /> | ||
| + | [[Value of polygamma at 1]]<br /> | ||
| + | [[Value of polygamma at positive integer]]<br /> | ||
| + | [[Value of polygamma at 1/2]]<br /> | ||
| + | [[Value of derivative of trigamma at positive integer plus 1/2]]<br /> | ||
| + | [[Relation between polygamma and Hurwitz zeta]]<br /> | ||
| + | [[Series for polygamma in terms of Riemann zeta]]<br /> | ||
=See Also= | =See Also= | ||
[[Digamma]]<br /> | [[Digamma]]<br /> | ||
[[Trigamma]]<br /> | [[Trigamma]]<br /> | ||
| + | |||
| + | =References= | ||
| + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=findme|next=Integral representation of polygamma for Re(z) greater than 0}}: $6.4.1$ | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Latest revision as of 22:47, 17 March 2017
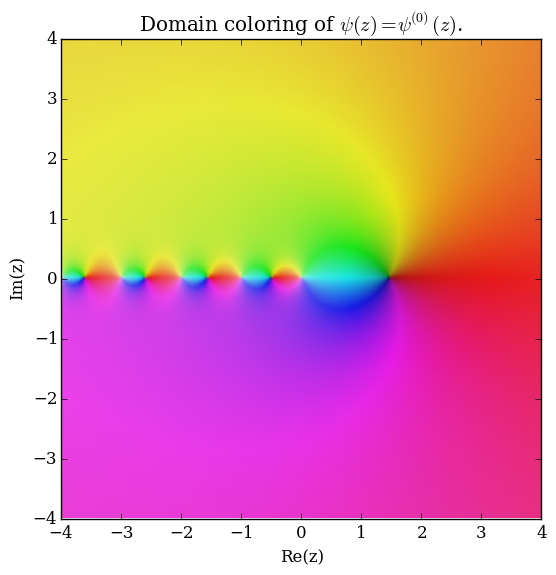
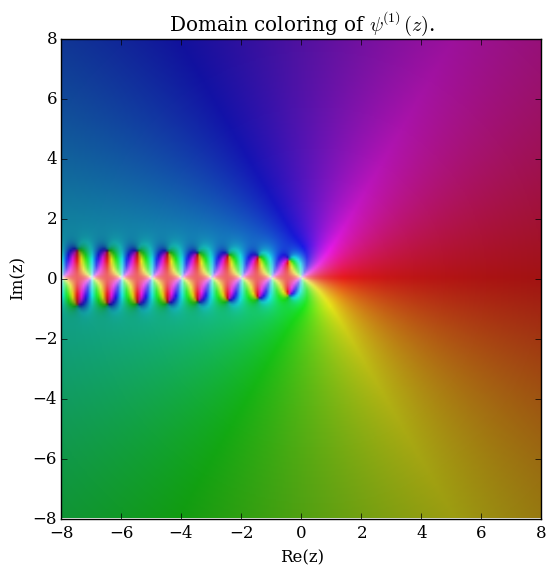
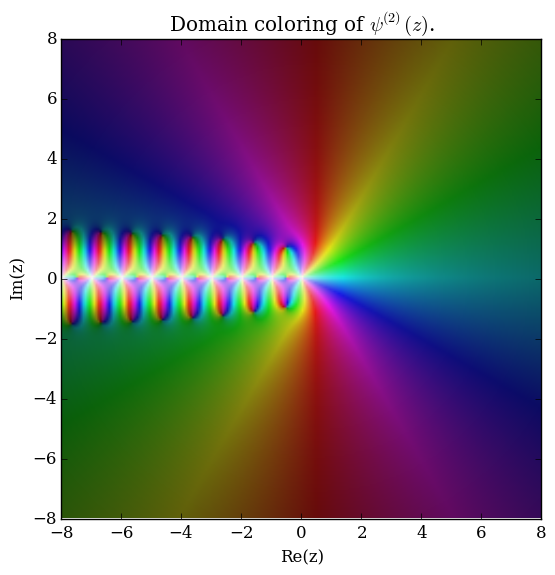
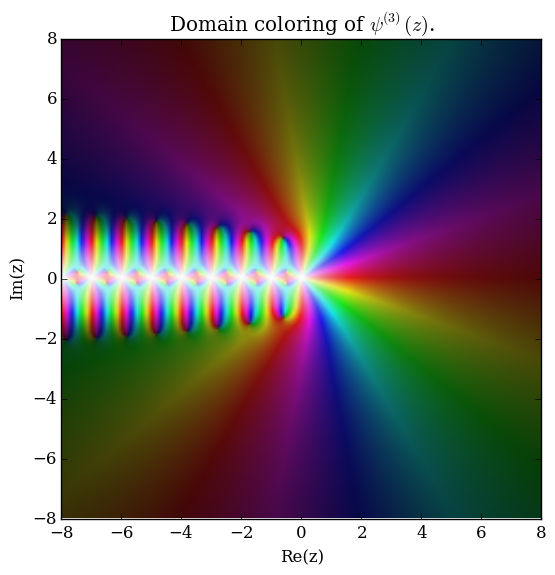
The polygamma function of order $m$, $\psi^{(m)}(z)$, is defined by the formula $$\psi^{(m)}(z) = \dfrac{\mathrm{d}^{m+1}}{\mathrm{d}z^{m+1}} \log \Gamma(z),$$ where $\log \Gamma$ denotes the loggamma function. The digamma function $\psi$ is the function $\psi^{(0)}(z)$ and the trigamma function is $\psi^{(1)}(z)$.
Domain coloring of $\psi^{(0)}(z)$.
Domain coloring of $\psi^{(1)}(z)$.
Domain coloring of $\psi^{(2)}(z)$.
Domain coloring of $\psi^{(3)}(z)$.
Domain coloring of $\psi^{(4)}(z)$.
Domain coloring of $\psi^{(5)}(z)$.
Properties
Integral representation of polygamma for Re(z) greater than 0
Integral representation of polygamma 2
Polygamma recurrence relation
Polygamma reflection formula
Polygamma multiplication formula
Polygamma series representation
Value of polygamma at 1
Value of polygamma at positive integer
Value of polygamma at 1/2
Value of derivative of trigamma at positive integer plus 1/2
Relation between polygamma and Hurwitz zeta
Series for polygamma in terms of Riemann zeta
See Also
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $6.4.1$
