Difference between revisions of "Cosine"
| (31 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | The cosine function, $\cos \colon \mathbb{ | + | The cosine function, $\cos \colon \mathbb{C} \rightarrow \mathbb{C}$ is defined by the formula |
| − | $$ | + | $$\cos(z)=\dfrac{e^{iz}+e^{-iz}}{2},$$ |
| + | where $e^z$ is the [[exponential function]]. | ||
| + | <div align="center"> | ||
<gallery> | <gallery> | ||
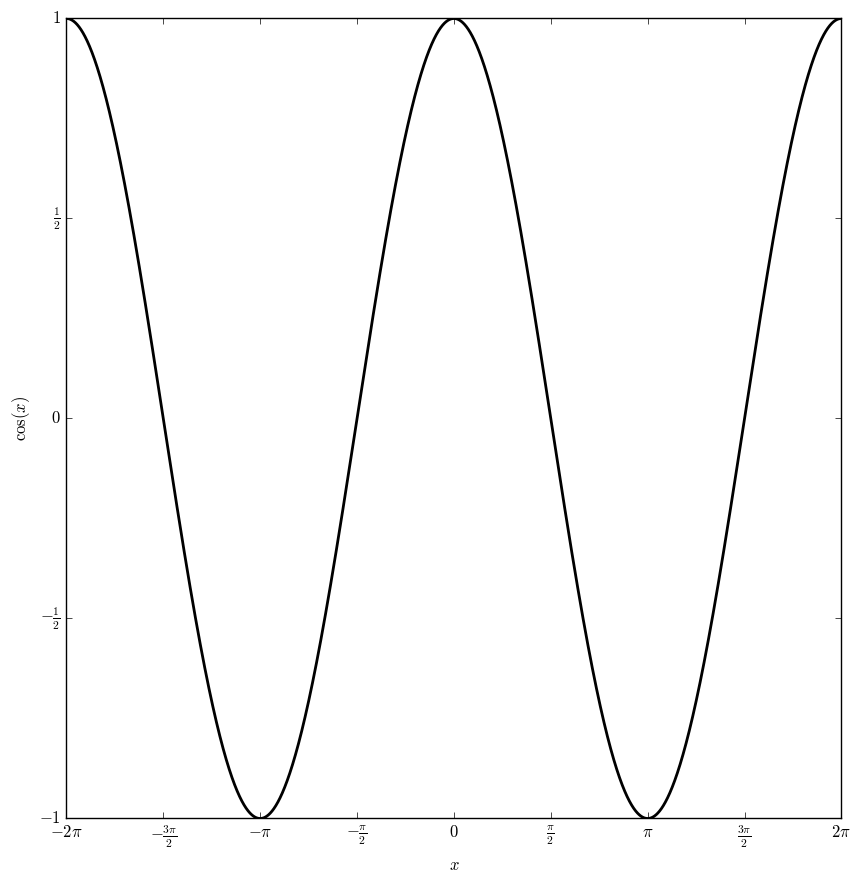
| − | File: | + | File:Cosineplot.png|Graph of $\cos$ on $[-2\pi,2\pi]$. |
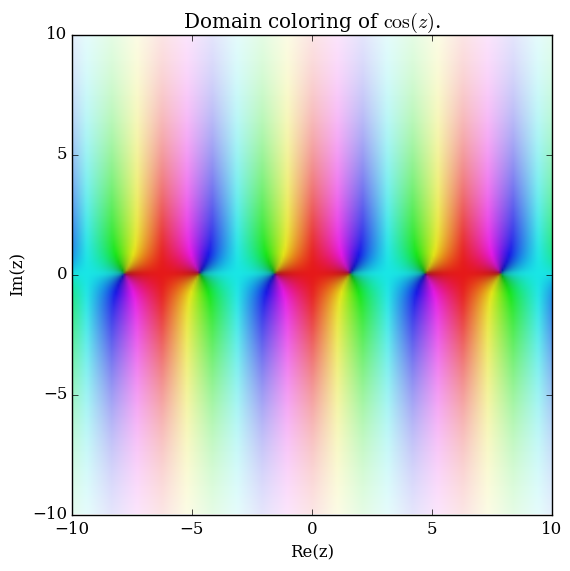
| − | File: | + | File:Complexcosineplot.png|[[Domain coloring]] of $\cos$. |
| + | File:Trig Functions Diagram.svg|Trig functions diagram using the unit circle. | ||
</gallery> | </gallery> | ||
| + | </div> | ||
| + | |||
| + | =Properties= | ||
| + | [[Derivative of cosine]]<br /> | ||
| + | [[Taylor series of cosine]]<br /> | ||
| + | [[Weierstrass factorization of cosine]]<br /> | ||
| + | [[Beta in terms of sine and cosine]]<br /> | ||
| + | [[Relationship between cosine and hypergeometric 0F1]]<br /> | ||
| + | [[Relationship between spherical Bessel y and cosine]]<br /> | ||
| + | [[Relationship between cosh and cos]]<br /> | ||
| + | [[Relationship between cos and cosh]]<br /> | ||
| + | [[Relationship between cosine, Gudermannian, and sech]]<br /> | ||
| + | [[Relationship between sech, inverse Gudermannian, and cos]]<br /> | ||
| + | [[2cos(mt)cos(nt)=cos((m+n)t)+cos((m-n)t)]]<br /> | ||
| + | [[Orthogonality relation for cosine on (0,pi)]]<br /> | ||
| + | |||
| + | =See Also= | ||
| + | [[Arccos]] <br /> | ||
| + | [[Cosh]] <br /> | ||
| + | [[Arccosh]] <br /> | ||
| + | |||
| + | =References= | ||
| + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Sine|next=Tangent}}: 4.3.2 | ||
| + | |||
| + | {{:Trigonometric functions footer}} | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 22:09, 19 December 2017
The cosine function, $\cos \colon \mathbb{C} \rightarrow \mathbb{C}$ is defined by the formula $$\cos(z)=\dfrac{e^{iz}+e^{-iz}}{2},$$ where $e^z$ is the exponential function.
Graph of $\cos$ on $[-2\pi,2\pi]$.
Domain coloring of $\cos$.
Trig functions diagram using the unit circle.
Properties
Derivative of cosine
Taylor series of cosine
Weierstrass factorization of cosine
Beta in terms of sine and cosine
Relationship between cosine and hypergeometric 0F1
Relationship between spherical Bessel y and cosine
Relationship between cosh and cos
Relationship between cos and cosh
Relationship between cosine, Gudermannian, and sech
Relationship between sech, inverse Gudermannian, and cos
2cos(mt)cos(nt)=cos((m+n)t)+cos((m-n)t)
Orthogonality relation for cosine on (0,pi)
See Also
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 4.3.2
