Difference between revisions of "Struve function"
(→Properties) |
|||
| Line 21: | Line 21: | ||
[[Recurrence relation for Struve function (2)]]<br /> | [[Recurrence relation for Struve function (2)]]<br /> | ||
[[Derivative of Struve H0]]<br /> | [[Derivative of Struve H0]]<br /> | ||
| + | [[d/dz(z^(-nu)H_(nu))=1/(sqrt(pi)2^(nu)Gamma(nu+3/2))-z^(-nu)H_(nu+1)]]<br /> | ||
=References= | =References= | ||
Revision as of 00:47, 21 December 2017
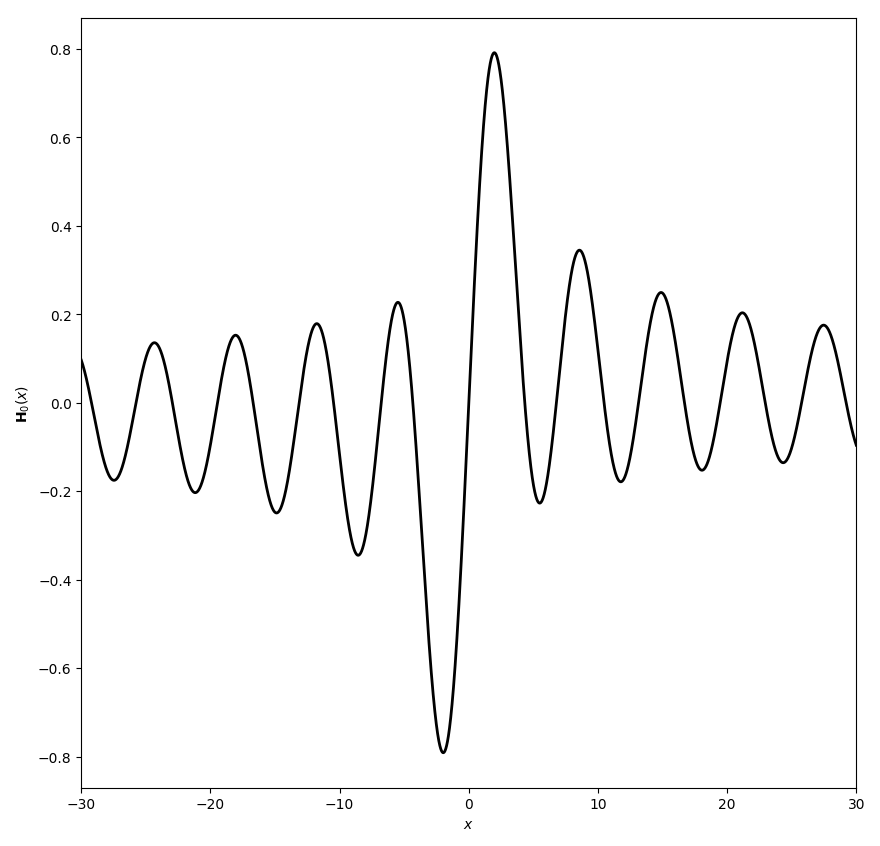
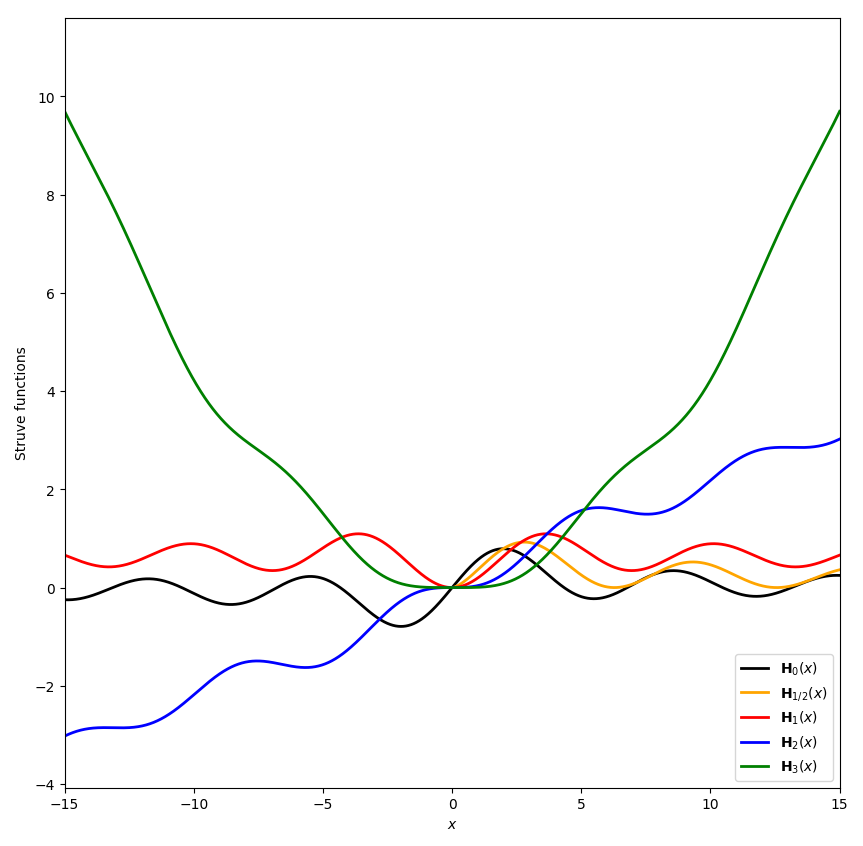
The Struve functions are defined by $$\mathbf{H}_{\nu}(z)=\left(\dfrac{z}{2}\right)^{\nu+1} \displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k\left(\frac{z}{2}\right)^{2k}}{\Gamma(k+\frac{3}{2})\Gamma \left(k+\nu+\frac{3}{2} \right)}.$$
Struve $\mathbf{H}_0$.
Various Struve functions.
Struve functions from Abramowitz&Stegun.
.png)
Properties
Relationship between Struve function and hypergeometric pFq
Relationship between Weber function 0 and Struve function 0
Relationship between Weber function 1 and Struve function 1
Integral representation of Struve function
Integral representation of Struve function (2)
Integral representation of Struve function (3)
Recurrence relation for Struve fuction
Recurrence relation for Struve function (2)
Derivative of Struve H0
d/dz(z^(-nu)H_(nu))=1/(sqrt(pi)2^(nu)Gamma(nu+3/2))-z^(-nu)H_(nu+1)
References
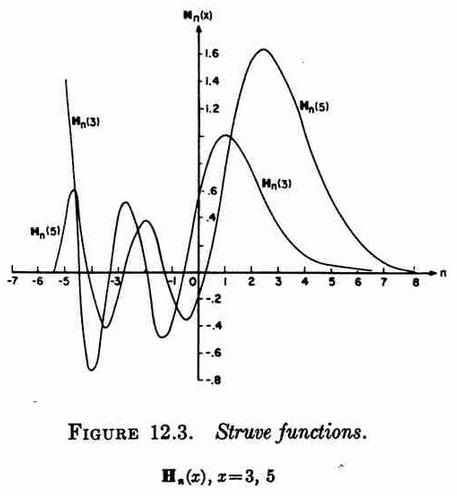
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $12.1.3$
