Difference between revisions of "Polygamma"

From specialfunctionswiki
Jump to: navigation, search
(→‎Properties)
 
(16 intermediate revisions by the same user not shown)
Line 1: Line 1:
 
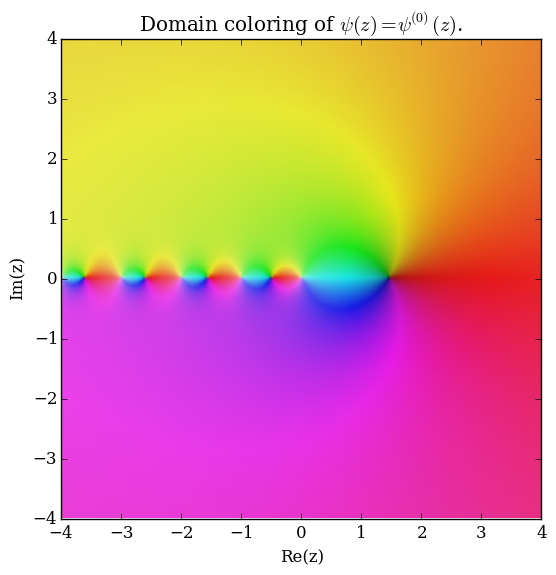
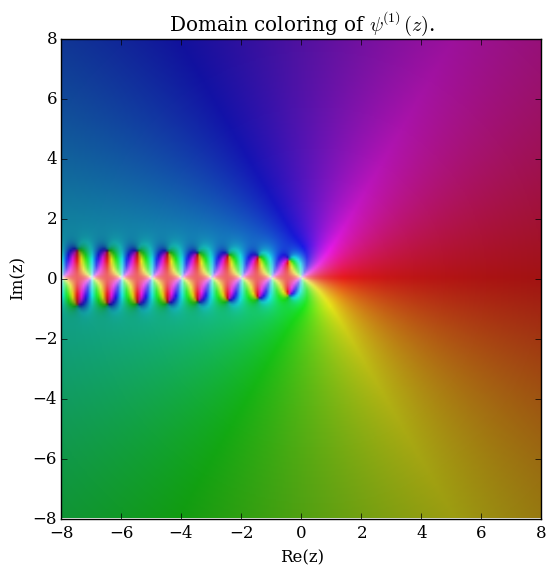
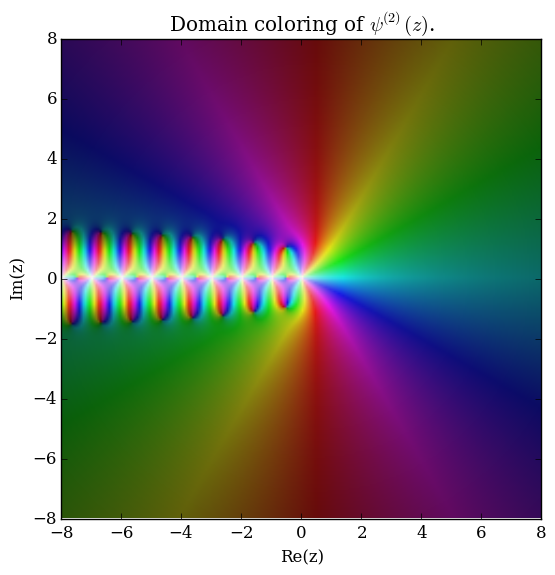
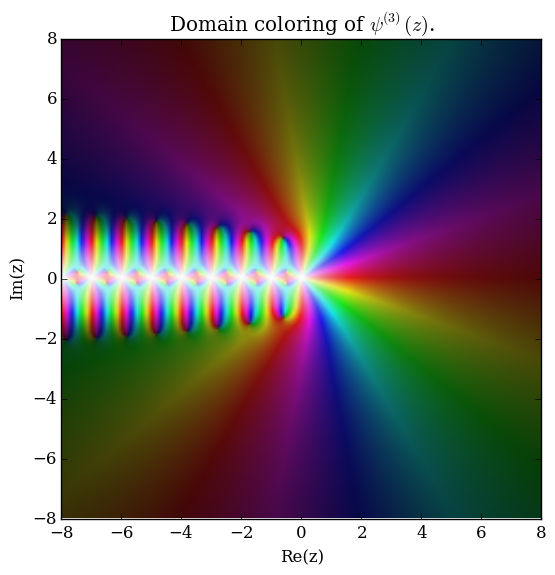
The polygamma function of order $m$, $\psi^{(m)}(z)$, is defined by the formula
 
The polygamma function of order $m$, $\psi^{(m)}(z)$, is defined by the formula
−
$$\psi^{(m)}(z) = \dfrac{d^m}{dz^m} \log \Gamma(z),$$
+
$$\psi^{(m)}(z) = \dfrac{\mathrm{d}^{m+1}}{\mathrm{d}z^{m+1}} \log \Gamma(z),$$
−
where $\log$ denotes the [[logarithm]] and $\log \Gamma$ denotes the [[loggamma]] function. The [[digamma]] function $\psi$ is the function $\psi^{(0)}(z)$ and the [[trigamma]] function is $\psi^{(1)}(z)$.
+
where $\log \Gamma$ denotes the [[loggamma]] function. The [[digamma]] function $\psi$ is the function $\psi^{(0)}(z)$ and the [[trigamma]] function is $\psi^{(1)}(z)$.
  
 
<div align="center">
 
<div align="center">
Line 13: Line 13:
 
</gallery>
 
</gallery>
 
</div>
 
</div>
 +
 +
=Properties=
 +
[[Integral representation of polygamma for Re(z) greater than 0]]<br />
 +
[[Integral representation of polygamma 2]]<br />
 +
[[Polygamma recurrence relation]]<br />
 +
[[Polygamma reflection formula]]<br />
 +
[[Polygamma multiplication formula]]<br />
 +
[[Polygamma series representation]]<br />
 +
[[Value of polygamma at 1]]<br />
 +
[[Value of polygamma at positive integer]]<br />
 +
[[Value of polygamma at 1/2]]<br />
 +
[[Value of derivative of trigamma at positive integer plus 1/2]]<br />
 +
[[Relation between polygamma and Hurwitz zeta]]<br />
 +
[[Series for polygamma in terms of Riemann zeta]]<br />
  
 
=See Also=
 
=See Also=
 
[[Digamma]]<br />
 
[[Digamma]]<br />
 
[[Trigamma]]<br />
 
[[Trigamma]]<br />
 +
 +
=References=
 +
* {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=findme|next=Integral representation of polygamma for Re(z) greater than 0}}: $6.4.1$
  
 
[[Category:SpecialFunction]]
 
[[Category:SpecialFunction]]

Latest revision as of 22:47, 17 March 2017

The polygamma function of order $m$, $\psi^{(m)}(z)$, is defined by the formula $$\psi^{(m)}(z) = \dfrac{\mathrm{d}^{m+1}}{\mathrm{d}z^{m+1}} \log \Gamma(z),$$ where $\log \Gamma$ denotes the loggamma function. The digamma function $\psi$ is the function $\psi^{(0)}(z)$ and the trigamma function is $\psi^{(1)}(z)$.

  • Domain coloring of $\psi^{(0)}(z)$.

  • Domain coloring of $\psi^{(1)}(z)$.

  • Domain coloring of $\psi^{(2)}(z)$.

  • Domain coloring of $\psi^{(3)}(z)$.

  • Domain coloring of $\psi^{(4)}(z)$.

  • Domain coloring of $\psi^{(5)}(z)$.

Properties

Integral representation of polygamma for Re(z) greater than 0
Integral representation of polygamma 2
Polygamma recurrence relation
Polygamma reflection formula
Polygamma multiplication formula
Polygamma series representation
Value of polygamma at 1
Value of polygamma at positive integer
Value of polygamma at 1/2
Value of derivative of trigamma at positive integer plus 1/2
Relation between polygamma and Hurwitz zeta
Series for polygamma in terms of Riemann zeta

See Also

Digamma
Trigamma

References

Retrieved from "http://specialfunctionswiki.org/index.php?title=Polygamma&oldid=8190"