Difference between revisions of "Kelvin ker"
From specialfunctionswiki
(Created page with "The $\mathrm{ker}_{\nu}$ function is defined as $$\mathrm{ber}(z)=\mathrm{Re} \hspace{2pt} K_{\nu} \left( x e^{\frac{\pi i}{4}} \right),$$ where $\mathrm{Re}$ denotes the re...") |
|||
| Line 2: | Line 2: | ||
$$\mathrm{ber}(z)=\mathrm{Re} \hspace{2pt} K_{\nu} \left( x e^{\frac{\pi i}{4}} \right),$$ | $$\mathrm{ber}(z)=\mathrm{Re} \hspace{2pt} K_{\nu} \left( x e^{\frac{\pi i}{4}} \right),$$ | ||
where $\mathrm{Re}$ denotes the [[real part]] of a [[complex number]] and $K_{\nu}$ denotes the [[Modified Bessel K sub nu|modified Bessel function $K_{\nu}$]]. | where $\mathrm{Re}$ denotes the [[real part]] of a [[complex number]] and $K_{\nu}$ denotes the [[Modified Bessel K sub nu|modified Bessel function $K_{\nu}$]]. | ||
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
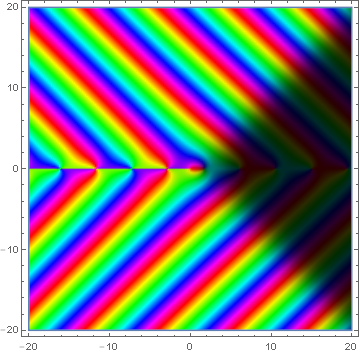
| + | File:Domcolkelvinkersub0.png|[[Domain coloring]] of $\mathrm{ker}_0$. | ||
| + | </gallery> | ||
| + | </div> | ||
Revision as of 03:17, 21 August 2015
The $\mathrm{ker}_{\nu}$ function is defined as $$\mathrm{ber}(z)=\mathrm{Re} \hspace{2pt} K_{\nu} \left( x e^{\frac{\pi i}{4}} \right),$$ where $\mathrm{Re}$ denotes the real part of a complex number and $K_{\nu}$ denotes the modified Bessel function $K_{\nu}$.
Domain coloring of $\mathrm{ker}_0$.