Difference between revisions of "Logarithm"
| Line 32: | Line 32: | ||
=See Also= | =See Also= | ||
| − | [[Logarithm (multivalued)]] | + | [[Dilogarithm]]<br /> |
| + | [[Logarithm (multivalued)]]<br /> | ||
| + | [[Polylogarithm]]<br /> | ||
=References= | =References= | ||
Revision as of 07:02, 4 June 2016
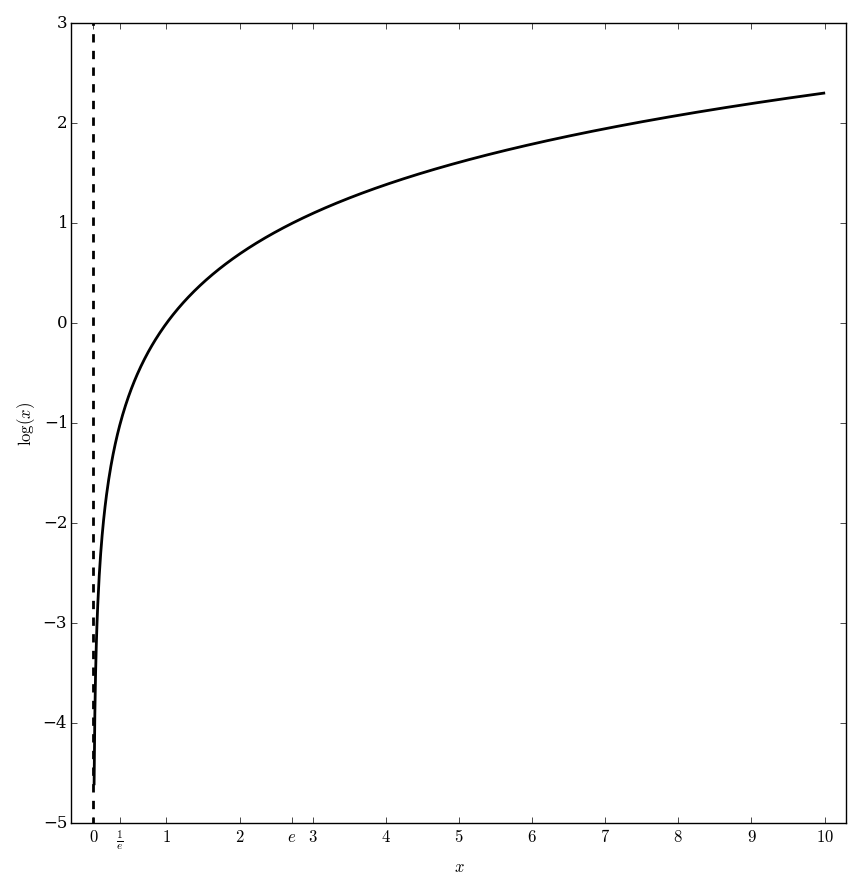
The (single-valued) logarithm $\log \colon \mathbb{C} \setminus (-\infty,0] \rightarrow \mathbb{C}$ defined by the formula $$\log(z) = \displaystyle\int_1^z \dfrac{1}{t} \mathrm{d}t,$$ where we understand the integral $\displaystyle\int_1^z$ as a contour integral over a path from $1$ to $z$ that does not intersect the set $(-\infty,0] \subset \mathbb{C}$. The logarithm restricted to $(0,\infty)$ is the inverse function of the exponential function restricted to $\mathbb{R}$.
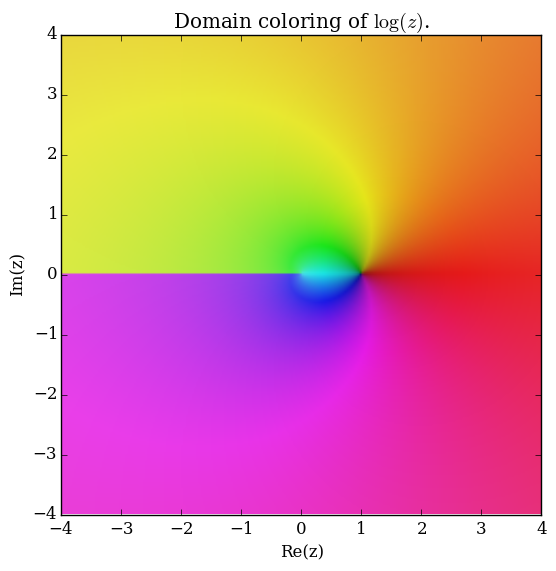
Domain coloring of $\log$.
Properties
Real and imaginary parts of log
Relationship between logarithm (multivalued) and logarithm
Logarithm of product is a sum of logarithms
Logarithm of a quotient is a difference of logarithms
Relationship between logarithm and positive integer exponents
Logarithm of 1
Logarithm diverges to negative infinity at 0 from right
Logarithm at minus 1
Logarithm at i
Logarithm at -i
Taylor series of $\log(1-z)$
Taylor series of $\log(1+z)$
Antiderivative of the logarithm
Z2F1(1,1;2,-z) equals log(1+z)
Exponential integral Ei series
Relationship between prime zeta, Möbius function, logarithm, and Riemann zeta
The prime number theorem
See Also
Dilogarithm
Logarithm (multivalued)
Polylogarithm
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 4.1.1