Kelvin ker
From specialfunctionswiki
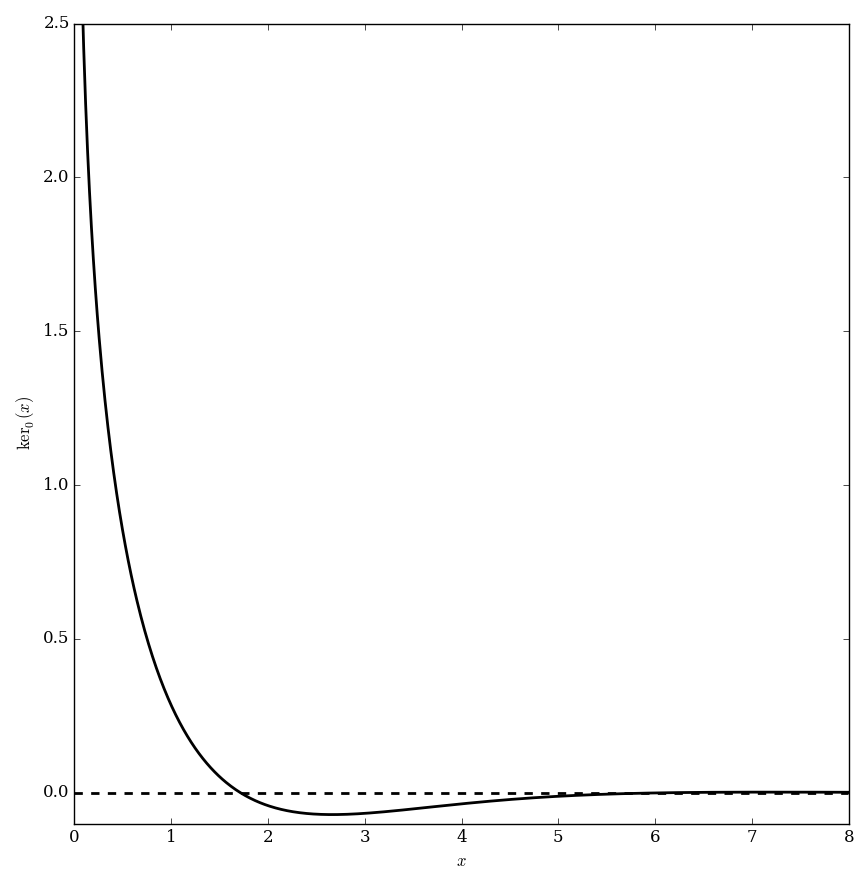
The $\mathrm{ker}_{\nu}$ function is defined as $$\mathrm{ker}_{\nu}(z)=\mathrm{Re} \left[ e^{-\frac{\nu \pi i}{2}} K_{\nu} \left( z e^{\frac{\pi i}{4}} \right) \right],$$ where $\mathrm{Re}$ denotes the real part of a complex number and $K_{\nu}$ denotes the modified Bessel function $K_{\nu}$.
Graph of $\mathrm{ker}_0$.
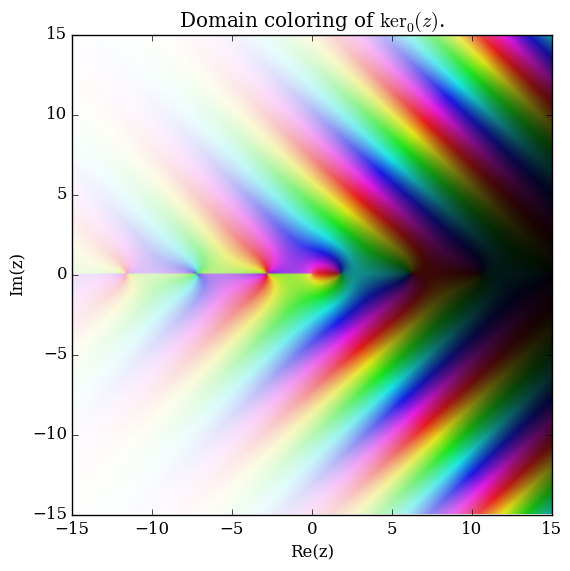
Domain coloring of $\mathrm{ker}_0$.
Properties
References
- 1953: Arthur Erdélyi, Wilhelm Magnus, Fritz Oberhettinger and Francesco G. Tricomi: Higher Transcendental Functions Volume II ... (previous) ... (next): $\S 7.2.3 (20)$
