Difference between revisions of "Beta"
| (37 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
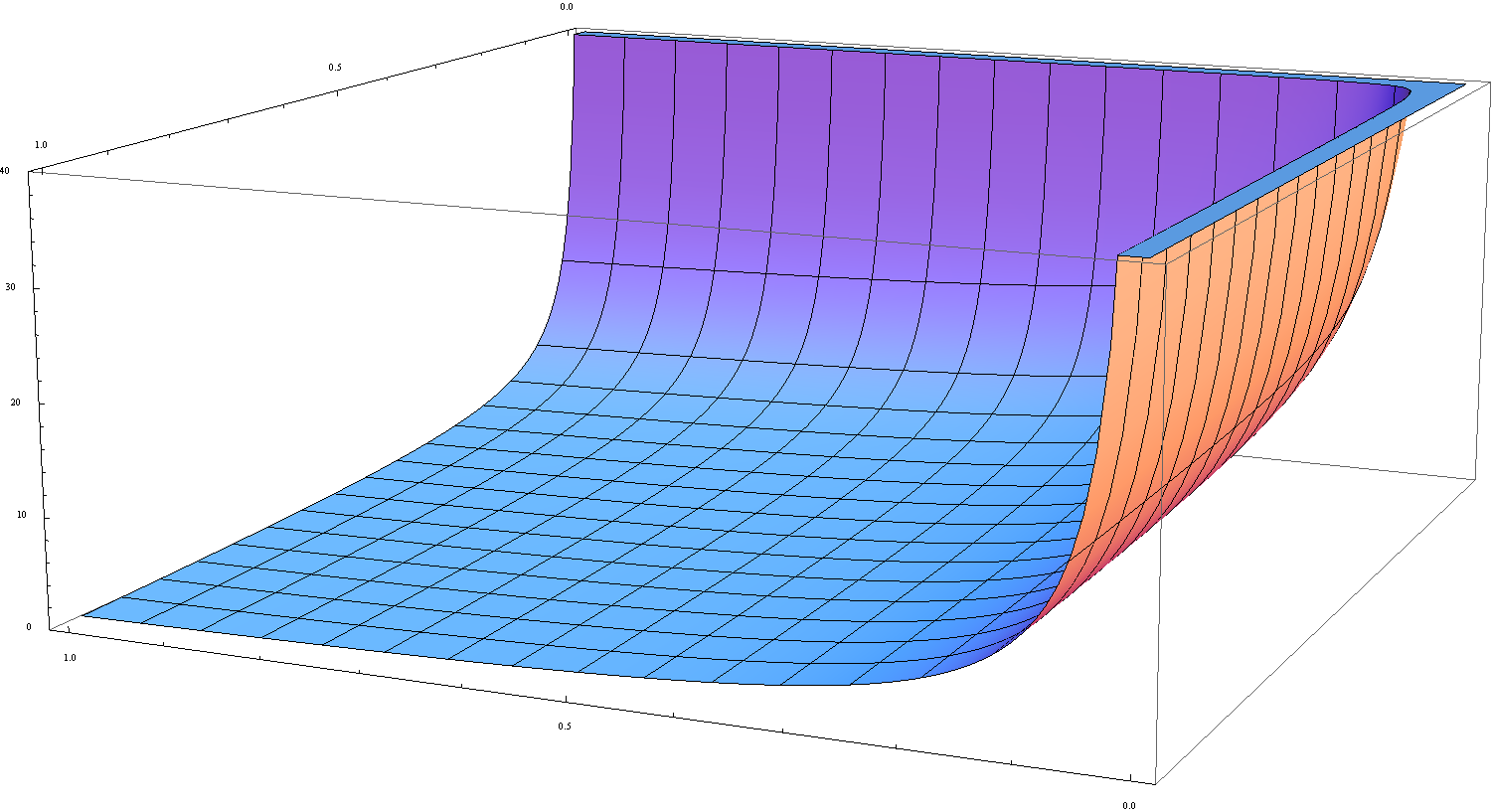
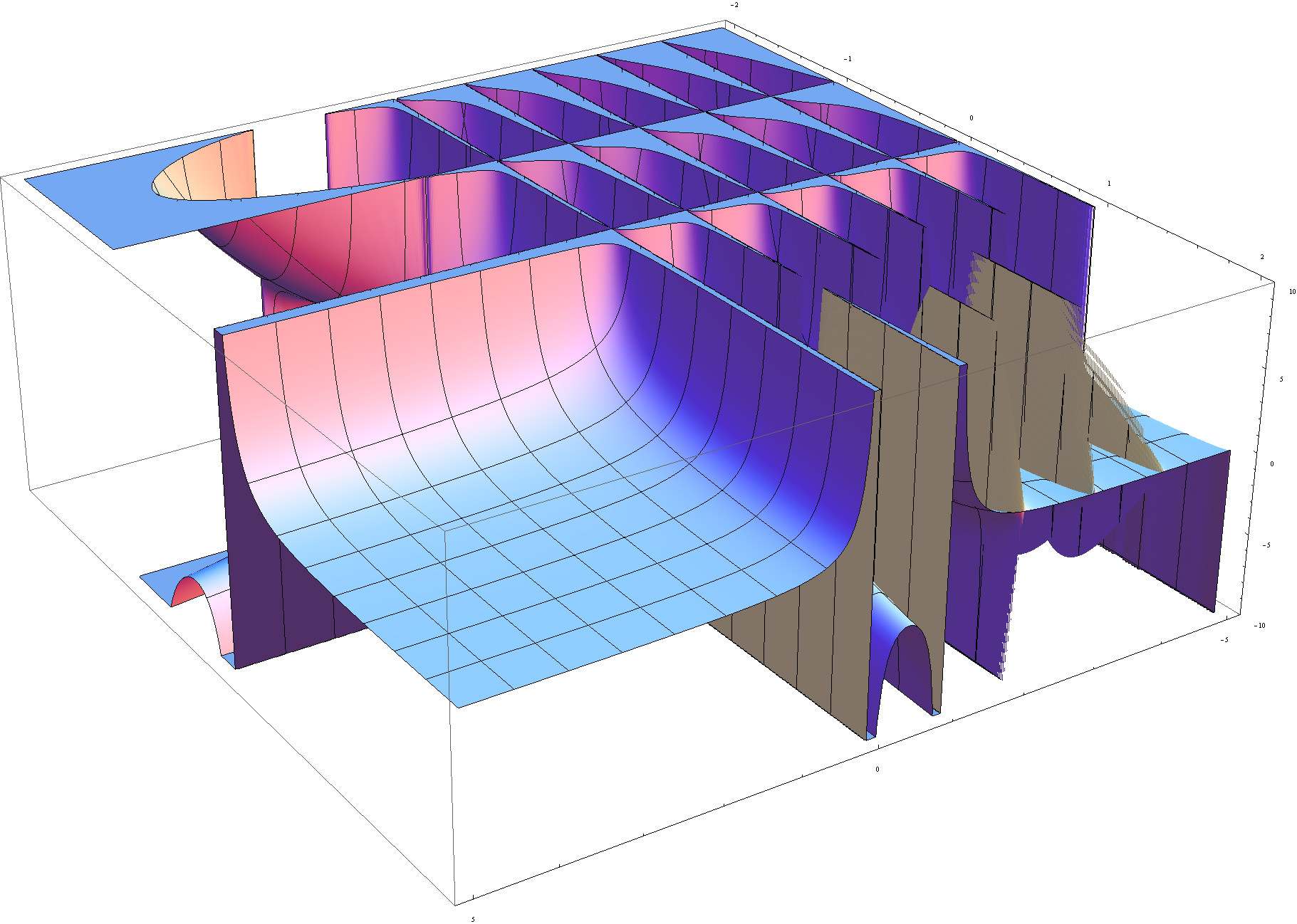
| − | The $\beta$ | + | The beta function $B$ (note: $B$ is [https://en.wikipedia.org/wiki/Beta capital $\beta$] in Greek) is defined by the following formula for $\mathrm{Re}(x)>0$ and $\mathrm{Re}(y)>0$: |
| − | $$B(x,y)=\displaystyle\int_0^1 t^{x-1}(1-t)^{y-1} | + | $$B(x,y)=\displaystyle\int_0^1 t^{x-1}(1-t)^{y-1} \mathrm{d}t.$$ |
| − | + | <div align="center"> | |
| − | + | <gallery> | |
| − | + | File:Beta2.png | |
| + | File:Beta.png | ||
| + | </gallery> | ||
| + | </div> | ||
=Properties= | =Properties= | ||
| − | < | + | [[Partial derivative of beta function]]<br /> |
| − | < | + | [[Beta in terms of gamma]]<br /> |
| − | + | [[Beta in terms of sine and cosine]]<br /> | |
| − | + | [[Beta as improper integral]]<br /> | |
| − | < | + | [[Beta is symmetric]]<br /> |
| − | < | + | [[B(x,y)=integral (t^(x-1)+t^(y-1))(1+t)^(-x-y) dt]]<br /> |
| − | </ | + | [[B(x,y+1)=(y/x)B(x+1,y)]]<br /> |
| − | </ | + | [[B(x,y+1)=(y/(x+y))B(x,y)]]<br /> |
| − | + | [[B(x,y)B(x+y,z)=B(y,z)B(y+z,x)]] <br /> | |
| − | + | [[B(x,y)B(x+y,z)=B(z,x)B(x+z,y)]]<br /> | |
| − | < | + | [[B(x,y)B(x+y,z)B(x+y+z,u)=Gamma(x)Gamma(y)Gamma(z)Gamma(u)/Gamma(x+y+z+u)]]<br /> |
| − | + | [[1/B(n,m)=m((n+m-1) choose (n-1))]] <br /> | |
| − | < | + | [[1/B(n,m)=n((n+m-1) choose (m-1))]]<br /> |
| − | </ | + | [[B(x,y)=2^(1-x-y)integral (1+t)^(x-1)(1-t)^(y-1)+(1+t)^(y-1)(1-t)^(x-1) dt]]<br /> |
| − | </ | + | [[Integral t^(x-1)(1-t)^(y-1)(1+bt)^(-x-y)dt = (1+b)^(-x)B(x,y)]]<br /> |
| + | [[Integral t^(x-1)(1+bt)^(-x-y) dt = b^(-x) B(x,y)]]<br /> | ||
| + | [[Integral (t-b)^(x-1)(a-t)^(y-1)dt=(a-b)^(x+y-1)B(x,y)]]<br /> | ||
| + | [[Integral of (t-b)^(x-1)(a-t)^(y-1)/(t-x)^(x+y) dt=(a-b)^(x+y-1)/((a-c)^x(b-c)^y) B(x,y)]]<br /> | ||
| + | [[Integral of (t-b)^(x-1)(a-t)^(y-1)/(c-t)^(x+y) dt = (a-b)^(x+y-1)/((c-a)^x (c-b)^y) B(x,y)]]<br /> | ||
| + | [[Integral of (1+bt^z)^(-y)t^x dt = (1/z)*b^(-(x+1)/z) B((x+1)/z,y-(x+1)/z)]]<br /> | ||
| + | [[Integral of t^(x-1)(1-t^z)^(y-1) dt=(1/z)B(x/z,y)]]<br /> | ||
| + | [[Integral of (1+t)^(2x-1)(1-t)^(2y-1)(1+t^2)^(-x-y)dt=2^(x+y-2)B(x,y)]]<br /> | ||
| − | + | =Videos= | |
| − | < | + | [https://www.youtube.com/watch?v=HP0kCw2FWJk Beta integral function - basic identity (5 December 2011)]<br /> |
| − | ( | + | [https://www.youtube.com/watch?v=VlROhSMiI2A Beta Function - Gamma Function Relation Part 1 (5 December 2011)]<br /> |
| − | < | + | [https://www.youtube.com/watch?v=fFxcrCaYR3k Beta Function - Gamma Function Relation Part 2 (5 December 2011)]<br /> |
| − | + | [https://www.youtube.com/watch?v=SYfLj-koGJ0 Beta function - Part 1 (14 February 2012)]<br /> | |
| − | </ | + | [https://www.youtube.com/watch?v=C3PmT6oNEew Mod-04 Lec-09 Analytic continuation and the gamma function (Part I) (3 June 2014)]<br /> |
| − | </ | + | [https://www.youtube.com/watch?v=Korx_G7eySQ Gamma function - Part 10 - Beta function (31 July 2012)]<br /> |
| + | [https://www.youtube.com/watch?v=3vBBh0SDpqM Beta function (19 September 2012)]<br /> | ||
| + | [https://www.youtube.com/watch?v=w0g9Ff9V7rs Gamma Function, Transformation of Gamma Function, Beta Function, Transformation of Beta Function (30 October 2012)]<br /> | ||
| + | [https://www.youtube.com/watch?v=uK0KUXVDqlQ Beta Integral: Even Powers Of Sine Function (26 December 2012)]<br /> | ||
=References= | =References= | ||
| − | + | * {{BookReference|Higher Transcendental Functions Volume I|1953|Arthur Erdélyi|author2=Wilhelm Magnus|author3=Fritz Oberhettinger|author4=Francesco G. Tricomi|prev=findme|next=Beta as improper integral}}: $\S 1.5 (1)$ | |
| + | * {{BookReference|Special Functions of Mathematical Physics and Chemistry|1956|Ian N. Sneddon|prev=Gamma|next=findme}}: $\S 5 (5.2)$ | ||
| + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=findme|next=Beta in terms of power of t over power of (1+t)}}: $6.2.1$ | ||
| + | * {{BookReference|Special Functions for Scientists and Engineers|1968|W.W. Bell|prev=Gamma|next=Gamma(1)=1}}: $(2.2)$ | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 19:49, 15 March 2018
The beta function $B$ (note: $B$ is capital $\beta$ in Greek) is defined by the following formula for $\mathrm{Re}(x)>0$ and $\mathrm{Re}(y)>0$: $$B(x,y)=\displaystyle\int_0^1 t^{x-1}(1-t)^{y-1} \mathrm{d}t.$$
Properties
Partial derivative of beta function
Beta in terms of gamma
Beta in terms of sine and cosine
Beta as improper integral
Beta is symmetric
B(x,y)=integral (t^(x-1)+t^(y-1))(1+t)^(-x-y) dt
B(x,y+1)=(y/x)B(x+1,y)
B(x,y+1)=(y/(x+y))B(x,y)
B(x,y)B(x+y,z)=B(y,z)B(y+z,x)
B(x,y)B(x+y,z)=B(z,x)B(x+z,y)
B(x,y)B(x+y,z)B(x+y+z,u)=Gamma(x)Gamma(y)Gamma(z)Gamma(u)/Gamma(x+y+z+u)
1/B(n,m)=m((n+m-1) choose (n-1))
1/B(n,m)=n((n+m-1) choose (m-1))
B(x,y)=2^(1-x-y)integral (1+t)^(x-1)(1-t)^(y-1)+(1+t)^(y-1)(1-t)^(x-1) dt
Integral t^(x-1)(1-t)^(y-1)(1+bt)^(-x-y)dt = (1+b)^(-x)B(x,y)
Integral t^(x-1)(1+bt)^(-x-y) dt = b^(-x) B(x,y)
Integral (t-b)^(x-1)(a-t)^(y-1)dt=(a-b)^(x+y-1)B(x,y)
Integral of (t-b)^(x-1)(a-t)^(y-1)/(t-x)^(x+y) dt=(a-b)^(x+y-1)/((a-c)^x(b-c)^y) B(x,y)
Integral of (t-b)^(x-1)(a-t)^(y-1)/(c-t)^(x+y) dt = (a-b)^(x+y-1)/((c-a)^x (c-b)^y) B(x,y)
Integral of (1+bt^z)^(-y)t^x dt = (1/z)*b^(-(x+1)/z) B((x+1)/z,y-(x+1)/z)
Integral of t^(x-1)(1-t^z)^(y-1) dt=(1/z)B(x/z,y)
Integral of (1+t)^(2x-1)(1-t)^(2y-1)(1+t^2)^(-x-y)dt=2^(x+y-2)B(x,y)
Videos
Beta integral function - basic identity (5 December 2011)
Beta Function - Gamma Function Relation Part 1 (5 December 2011)
Beta Function - Gamma Function Relation Part 2 (5 December 2011)
Beta function - Part 1 (14 February 2012)
Mod-04 Lec-09 Analytic continuation and the gamma function (Part I) (3 June 2014)
Gamma function - Part 10 - Beta function (31 July 2012)
Beta function (19 September 2012)
Gamma Function, Transformation of Gamma Function, Beta Function, Transformation of Beta Function (30 October 2012)
Beta Integral: Even Powers Of Sine Function (26 December 2012)
References
- 1953: Arthur Erdélyi, Wilhelm Magnus, Fritz Oberhettinger and Francesco G. Tricomi: Higher Transcendental Functions Volume I ... (previous) ... (next): $\S 1.5 (1)$
- 1956: Ian N. Sneddon: Special Functions of Mathematical Physics and Chemistry ... (previous) ... (next): $\S 5 (5.2)$
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $6.2.1$
- 1968: W.W. Bell: Special Functions for Scientists and Engineers ... (previous) ... (next): $(2.2)$