Difference between revisions of "Logarithm"
| (44 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | __NOTOC__ | |
| − | $$\log( | + | The (single-valued) logarithm $\log \colon \mathbb{C} \setminus (-\infty,0] \rightarrow \mathbb{C}$ defined by the formula |
| − | + | $$\log(z) = \displaystyle\int_1^z \dfrac{1}{t} \mathrm{d}t,$$ | |
| + | where we understand the integral $\displaystyle\int_1^z$ as a contour integral over a path from $1$ to $z$ that does not intersect the set $(-\infty,0] \subset \mathbb{C}$. | ||
| − | + | <div align="center"> | |
| − | <div | + | <gallery> |
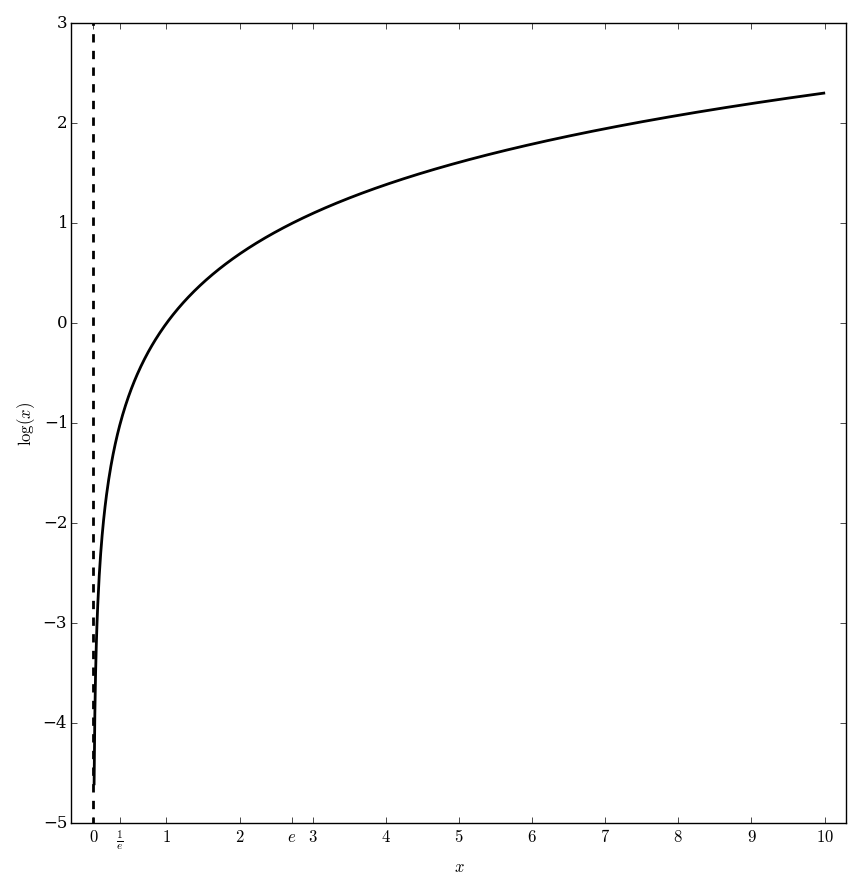
| − | < | + | File:Logarithmplot.png|Graph of $\log$ on $(0,10]$. |
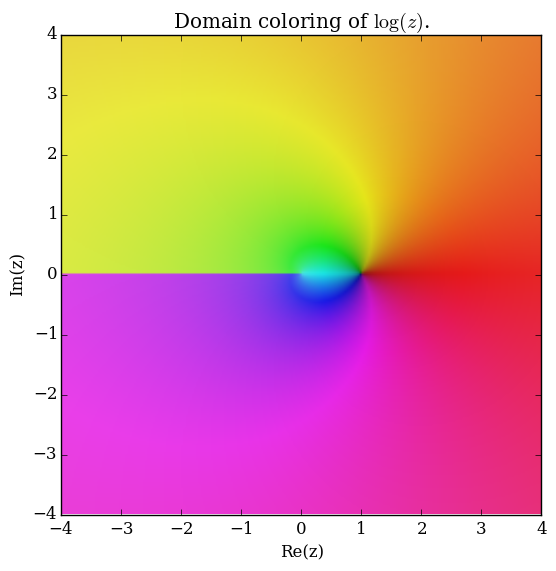
| − | + | File:Complexlogarithm.png|[[Domain coloring]] of $\log$. | |
| − | + | </gallery> | |
| − | </ | ||
</div> | </div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | =Properties= | ||
| + | [[Logarithm of a complex number]]<br /> | ||
| + | [[Derivative of the logarithm]]<br /> | ||
| + | [[Real and imaginary parts of log]]<br /> | ||
| + | [[Relationship between logarithm (multivalued) and logarithm]]<br /> | ||
| + | [[Logarithm of product is a sum of logarithms]]<br /> | ||
| + | [[Logarithm of a quotient is a difference of logarithms]]<br /> | ||
| + | [[Relationship between logarithm and positive integer exponents]]<br /> | ||
| + | [[Logarithm of 1]]<br /> | ||
| + | [[Logarithm diverges to negative infinity at 0 from right]]<br /> | ||
| + | [[Logarithm at minus 1]]<br /> | ||
| + | [[Logarithm at i]]<br /> | ||
| + | [[Logarithm at -i]]<br /> | ||
| + | [[Taylor series of log(1-z)|Taylor series of $\log(1-z)$]] <br /> | ||
| + | [[Taylor series of log(1+z)|Taylor series of $\log(1+z)$]]<br /> | ||
| + | [[Antiderivative of the logarithm]]<br /> | ||
| + | [[Z2F1(1,1;2,-z) equals log(1+z)]]<br /> | ||
| + | [[Exponential integral Ei series]]<br /> | ||
| + | [[Relationship between prime zeta, Möbius function, logarithm, and Riemann zeta]]<br /> | ||
| + | [[Prime number theorem, pi and x/log(x)|The prime number theorem]]<br /> | ||
| + | [[Series for log(z) for Re(z) greater than 1/2]]<br /> | ||
| + | [[Series for log(z) for absolute value of (z-1) less than 1]]<br /> | ||
| + | [[Series for log(z) for Re(z) greater than 0]]<br /> | ||
| + | [[Laurent series for log((z+1)/(z-1)) for absolute value of z greater than 1]]<br /> | ||
| + | [[Series for log(z+a) for positive a and Re(z) greater than -a]]<br /> | ||
| + | [[Relationship between logarithm and Mangoldt]]<br /> | ||
| + | [[Log e(z)=log(z)]]<br /> | ||
| + | [[Log 10(z)=log(z)/log(10)]]<br /> | ||
| + | [[Log 10(z)=log 10(e)log(z)]]<br /> | ||
| + | [[Log(z)=log(10)log 10(z)]]<br /> | ||
| + | [[Limit of log(x)/x^a=0]]<br /> | ||
| + | [[Limit of x^a log(x)=0]]<br /> | ||
| + | [[X/(1+x) less than log(1+x)]]<br /> | ||
| + | [[Log(1+x) less than x]]<br /> | ||
| + | [[X less than -log(1-x)]]<br /> | ||
| + | [[-log(1-x) less than x/(1-x)]]<br /> | ||
| + | [[Abs(log(1-x)) less than 3x/2]]<br /> | ||
| + | [[Log(x) less than or equal to x-1]]<br /> | ||
| + | [[Log(x) less than or equal to n(x^(1/n)-1)]]<br /> | ||
| + | [[Abs(log(1+z)) less than or equal to -log(1-abs(z))]]<br /> | ||
| + | [[Log(1+z) as continued fraction]]<br /> | ||
| + | [[Log((1+z)/(1-z)) as continued fraction]]<br /> | ||
| + | |||
| + | =References= | ||
| + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Continued fraction|next=Real and imaginary parts of log}}: $4.1.1$ | ||
| + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Nth derivative of logarithm|next=Antiderivative of the logarithm}}: $4.1.48$ | ||
| − | + | {{:Logarithm and friends footer}} | |
| − | {{: | ||
| − | |||
| − | |||
| − | + | [[Category:SpecialFunction]] | |
| − | [[ | ||
Latest revision as of 05:03, 21 December 2017
The (single-valued) logarithm $\log \colon \mathbb{C} \setminus (-\infty,0] \rightarrow \mathbb{C}$ defined by the formula $$\log(z) = \displaystyle\int_1^z \dfrac{1}{t} \mathrm{d}t,$$ where we understand the integral $\displaystyle\int_1^z$ as a contour integral over a path from $1$ to $z$ that does not intersect the set $(-\infty,0] \subset \mathbb{C}$.
Domain coloring of $\log$.
Properties
Logarithm of a complex number
Derivative of the logarithm
Real and imaginary parts of log
Relationship between logarithm (multivalued) and logarithm
Logarithm of product is a sum of logarithms
Logarithm of a quotient is a difference of logarithms
Relationship between logarithm and positive integer exponents
Logarithm of 1
Logarithm diverges to negative infinity at 0 from right
Logarithm at minus 1
Logarithm at i
Logarithm at -i
Taylor series of $\log(1-z)$
Taylor series of $\log(1+z)$
Antiderivative of the logarithm
Z2F1(1,1;2,-z) equals log(1+z)
Exponential integral Ei series
Relationship between prime zeta, Möbius function, logarithm, and Riemann zeta
The prime number theorem
Series for log(z) for Re(z) greater than 1/2
Series for log(z) for absolute value of (z-1) less than 1
Series for log(z) for Re(z) greater than 0
Laurent series for log((z+1)/(z-1)) for absolute value of z greater than 1
Series for log(z+a) for positive a and Re(z) greater than -a
Relationship between logarithm and Mangoldt
Log e(z)=log(z)
Log 10(z)=log(z)/log(10)
Log 10(z)=log 10(e)log(z)
Log(z)=log(10)log 10(z)
Limit of log(x)/x^a=0
Limit of x^a log(x)=0
X/(1+x) less than log(1+x)
Log(1+x) less than x
X less than -log(1-x)
-log(1-x) less than x/(1-x)
Abs(log(1-x)) less than 3x/2
Log(x) less than or equal to x-1
Log(x) less than or equal to n(x^(1/n)-1)
Abs(log(1+z)) less than or equal to -log(1-abs(z))
Log(1+z) as continued fraction
Log((1+z)/(1-z)) as continued fraction
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $4.1.1$
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $4.1.48$