Difference between revisions of "Struve function"
| (7 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
The Struve functions are defined by | The Struve functions are defined by | ||
| − | $$\mathbf{H}_{\nu}(z)=\left(\dfrac{z}{2}\right)^{\nu+1} \displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k\left(\frac{z}{2}\right)^{2k}}{\Gamma(k+\frac{3}{2})\Gamma(k+\nu+\frac{3}{2})}$$ | + | $$\mathbf{H}_{\nu}(z)=\left(\dfrac{z}{2}\right)^{\nu+1} \displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k\left(\frac{z}{2}\right)^{2k}}{\Gamma(k+\frac{3}{2})\Gamma \left(k+\nu+\frac{3}{2} \right)}.$$ |
<div align="center"> | <div align="center"> | ||
<gallery> | <gallery> | ||
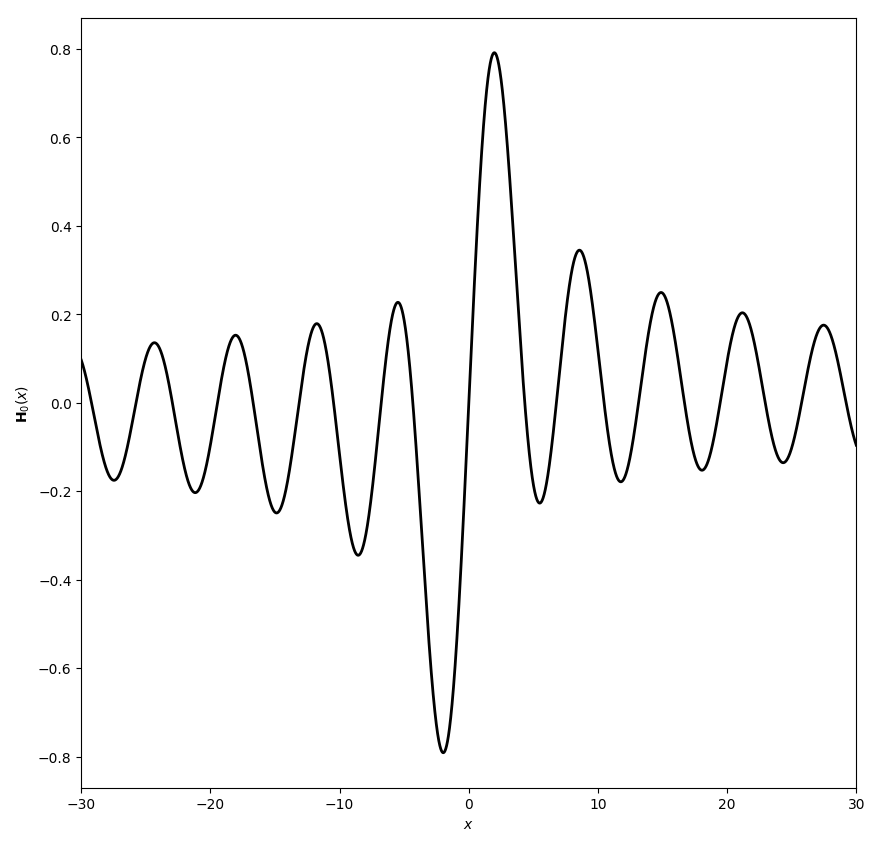
| + | File:Struveh0plot.png|Struve $\mathbf{H}_0$. | ||
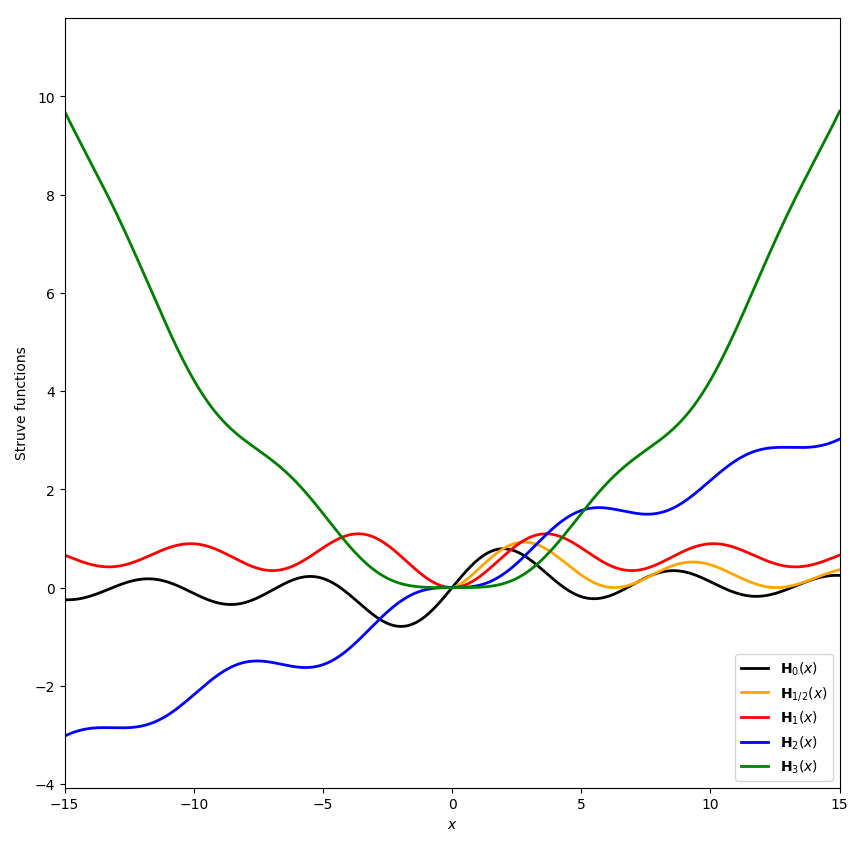
| + | File:Struveplots.png|Various Struve functions. | ||
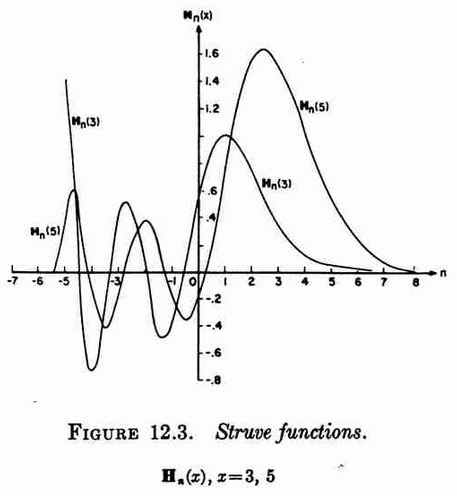
File:Struvefunctions(abramowitzandstegun).png|Struve functions from Abramowitz&Stegun. | File:Struvefunctions(abramowitzandstegun).png|Struve functions from Abramowitz&Stegun. | ||
</gallery> | </gallery> | ||
| Line 10: | Line 12: | ||
=Properties= | =Properties= | ||
| − | < | + | [[Relationship between Struve function and hypergeometric pFq]]<br /> |
| − | < | + | [[Relationship between Weber function 0 and Struve function 0]]<br /> |
| − | < | + | [[Relationship between Weber function 1 and Struve function 1]]<br /> |
| − | < | + | [[Integral representation of Struve function]]<br /> |
| − | </ | + | [[Integral representation of Struve function (2)]]<br /> |
| − | </ | + | [[Integral representation of Struve function (3)]]<br /> |
| − | + | [[Recurrence relation for Struve fuction]]<br /> | |
| − | + | [[Recurrence relation for Struve function (2)]]<br /> | |
| − | + | [[Derivative of Struve H0]]<br /> | |
| − | < | + | [[D/dz(z^(nu)H (nu))=z^(nu)H (nu-1)]]<br /> |
| − | < | + | [[D/dz(z^(-nu)H (nu))=1/(sqrt(pi)2^(nu)Gamma(nu+3/2))-z^(-nu)H (nu+1)]]<br /> |
| − | + | [[H (nu)(x) geq 0 for x gt 0 and nu geq 1/2]]<br /> | |
| − | + | [[H (-(n+1/2))(z)=(-1)^n J (n+1/2)(z) for integer n geq 0]]<br /> | |
| − | + | [[H (1/2)(z)=sqrt(2/(pi z))(1-cos(z))]]<br /> | |
| − | + | [[H (3/2)(z)=sqrt(z/(2pi))(1+2/z^2)-sqrt(2/(pi z))(sin(z)+cos(z)/z)]]<br /> | |
| − | </ | ||
| − | |||
| − | |||
| − | |||
=References= | =References= | ||
| − | + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=findme|next=Struve H0}}: $12.1.3$ | |
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Latest revision as of 01:09, 21 December 2017
The Struve functions are defined by $$\mathbf{H}_{\nu}(z)=\left(\dfrac{z}{2}\right)^{\nu+1} \displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k\left(\frac{z}{2}\right)^{2k}}{\Gamma(k+\frac{3}{2})\Gamma \left(k+\nu+\frac{3}{2} \right)}.$$
Struve $\mathbf{H}_0$.
Various Struve functions.
Struve functions from Abramowitz&Stegun.
.png)
Properties
Relationship between Struve function and hypergeometric pFq
Relationship between Weber function 0 and Struve function 0
Relationship between Weber function 1 and Struve function 1
Integral representation of Struve function
Integral representation of Struve function (2)
Integral representation of Struve function (3)
Recurrence relation for Struve fuction
Recurrence relation for Struve function (2)
Derivative of Struve H0
D/dz(z^(nu)H (nu))=z^(nu)H (nu-1)
D/dz(z^(-nu)H (nu))=1/(sqrt(pi)2^(nu)Gamma(nu+3/2))-z^(-nu)H (nu+1)
H (nu)(x) geq 0 for x gt 0 and nu geq 1/2
H (-(n+1/2))(z)=(-1)^n J (n+1/2)(z) for integer n geq 0
H (1/2)(z)=sqrt(2/(pi z))(1-cos(z))
H (3/2)(z)=sqrt(z/(2pi))(1+2/z^2)-sqrt(2/(pi z))(sin(z)+cos(z)/z)
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $12.1.3$
